Stochastic Financial Models

• A1.11 B1.16

  Stochastic Financial Models

  Part II, 2001

  (i) The price of the stock in the binomial model at time $r, 1 \leqslant r \leqslant n$, is $S_{r}=S_{0} \prod_{j=1}^{r} Y_{j}$, where $Y_{1}, Y_{2}, \ldots, Y_{n}$ are independent, identically-distributed random variables with $\mathbb{P}\left(Y_{1}=u\right)=p=1-\mathbb{P}\left(Y_{1}=d\right)$ and the initial price $S_{0}$ is a constant. Denote the fixed interest rate on the bank account by $\rho$, where $u>1+\rho>d>0$, and let the discount factor $\alpha=1 /(1+\rho)$. Determine the unique value $p=\bar{p}$ for which the sequence $\left\{\alpha^{r} S_{r}, 0 \leqslant r \leqslant n\right\}$ is a martingale.

  Explain briefly the significance of $\bar{p}$ for the pricing of contingent claims in the model.

  (ii) Let $T_{a}$ denote the first time that a standard Brownian motion reaches the level $a>0$. Prove that for $t>0$,

  $$\mathbb{P}\left(T_{a} \leqslant t\right)=2[1-\Phi(a / \sqrt{t})],$$

  where $\Phi$ is the standard normal distribution function.

  Suppose that $A_{t}$ and $B_{t}$ represent the prices at time $t$ of two different stocks with initial prices 1 and 2 , respectively; the prices evolve so that they may be represented as $A_{t}=e^{\sigma_{1} X_{t}+\mu t}$ and $B_{t}=2 e^{\sigma_{2} Y_{t}+\mu t}$, respectively, where $\left\{X_{t}\right\}_{t \geqslant 0}$ and $\left\{Y_{t}\right\}_{t \geqslant 0}$ are independent standard Brownian motions and $\sigma_{1}, \sigma_{2}$ and $\mu$ are constants. Let $T$ denote the first time, if ever, that the prices of the two stocks are the same. Determine $\mathbb{P}(T \leqslant t)$, for $t>0$.

  comment

• A3.11 B3.16

  Stochastic Financial Models

  Part II, 2001

  (i) Suppose that $Z$ is a random variable having the normal distribution with $\mathbb{E} Z=\beta$ and $\operatorname{Var} Z=\tau^{2}$.

  For positive constants $a, c$ show that

  $$\mathbb{E}\left(a e^{Z}-c\right)_{+}=a e^{\left(\beta+\tau^{2} / 2\right)} \Phi\left(\frac{\log (a / c)+\beta}{\tau}+\tau\right)-c \Phi\left(\frac{\log (a / c)+\beta}{\tau}\right)$$

  where $\Phi$ is the standard normal distribution function.

  In the context of the Black-Scholes model, derive the formula for the price at time 0 of a European call option on the stock at strike price $c$ and maturity time $t_{0}$ when the interest rate is $\rho$ and the volatility of the stock is $\sigma$.

  (ii) Let $p$ denote the price of the call option in the Black-Scholes model specified in (i). Show that $\frac{\partial p}{\partial \rho}>0$ and sketch carefully the dependence of $p$ on the volatility $\sigma$ (when the other parameters in the model are held fixed).

  Now suppose that it is observed that the interest rate lies in the range $0<\rho<\rho_{0}$ and when it changes it is linked to the volatility by the formula $\sigma=\ln \left(\rho_{0} / \rho\right)$. Consider a call option at strike price $c=S_{0}$, where $S_{0}$ is the stock price at time 0 . There is a small increase $\Delta \rho$ in the interest rate; will the price of the option increase or decrease (assuming that the stock price is unaffected)? Justify your answer carefully.

  [You may assume that the function $\phi(x) / \Phi(x)$ is decreasing in $x,-\infty<x<\infty$, and increases to $+\infty$ as $x \rightarrow-\infty$, where $\Phi$ is the standard-normal distribution function and $\phi=\Phi^{\prime}$.]

  comment

• A4.12 B4.16

  Stochastic Financial Models

  Part II, 2001

  Write an essay on the mean-variance approach to portfolio selection in a one-period model. Your essay should contrast the solution in the case when all the assets are risky with that for the case when there is a riskless asset.

  comment

• A1.11 B1.16

  Stochastic Financial Models

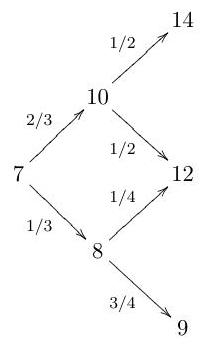
  Part II, 2002

  (i) The prices, $S_{i}$, of a stock in a binomial model at times $i=0,1,2$ are represented by the following binomial tree.

  

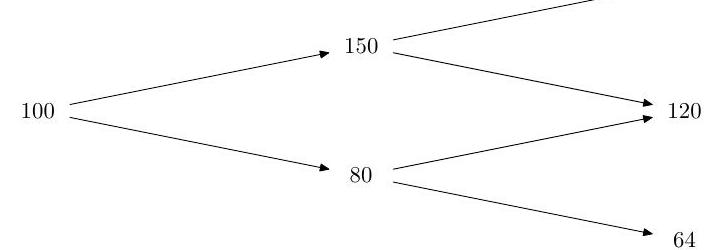
  The fixed interest rate per period is $1 / 5$ and the probability that the stock price increases in a period is $1 / 3$. Find the price at time 0 of a European call option with strike price 78 and expiry time $2 .$

  Explain briefly the ideas underlying your calculations.

  (ii) Consider an investor in a one-period model who may invest in $s$ assets, all of which are risky, with a random return vector $\boldsymbol{R}$ having mean $\mathbb{E} \boldsymbol{R}=\boldsymbol{r}$ and positivedefinite covariance matrix $\boldsymbol{V}$; assume that not all the assets have the same expected return. Show that any minimum-variance portfolio is equivalent to the investor dividing his wealth between two portfolios, the global minimum-variance portfolio and the diversified portfolio, both of which should be specified clearly in terms of $\boldsymbol{r}$ and $\boldsymbol{V}$.

  Now suppose that $\boldsymbol{R}=\left(R_{1}, R_{2}, \ldots, R_{s}\right)^{\top}$ where $R_{1}, R_{2}, \ldots, R_{s}$ are independent random variables with $R_{i}$ having the exponential distribution with probability density function $\lambda_{i} e^{-\lambda_{i} x}, x \geqslant 0$, where $\lambda_{i}>0,1 \leqslant i \leqslant s$. Determine the global minimum-variance portfolio and the diversified portfolio explicitly.

  Consider further the situation when the investor has the utility function $u(x)=$ $1-e^{-x}$, where $x$ denotes his wealth. Suppose that he acts to maximize the expected utility of his final wealth, and that his initial wealth is $w>0$. Show that he now divides his wealth between the diversified portfolio and the uniform portfolio, in which wealth is apportioned equally between the assets, and determine the amounts that he invests in each.

  comment

• A3.11 B3.16

  Stochastic Financial Models

  Part II, 2002

  (i) Explain briefly what it means to say that a stochastic process $\left\{W_{t}, t \geqslant 0\right\}$ is a standard Brownian motion.

  Let $\left\{W_{t}, t \geqslant 0\right\}$ be a standard Brownian motion and let $a, b$ be real numbers. What condition must $a$ and $b$ satisfy to ensure that the process $e^{a W_{t}+b t}$ is a martingale? Justify your answer carefully.

  (ii) At the beginning of each of the years $r=0,1, \ldots, n-1$ an investor has income $X_{r}$, of which he invests a proportion $\rho_{r}, 0 \leqslant \rho_{r} \leqslant 1$, and consumes the rest during the year. His income at the beginning of the next year is

  $$X_{r+1}=X_{r}+\rho_{r} X_{r} W_{r}$$

  where $W_{0}, \ldots, W_{n-1}$ are independent positive random variables with finite means and $X_{0} \geqslant 0$ is a constant. He decides on $\rho_{r}$ after he has observed both $X_{r}$ and $W_{r}$ at the beginning of year $r$, but at that time he does not have any knowledge of the value of $W_{s}$, for any $s>r$. The investor retires in year $n$ and consumes his entire income during that year. He wishes to determine the investment policy that maximizes his expected total consumption

  $$\mathbb{E}\left[\sum_{r=0}^{n-1}\left(1-\rho_{r}\right) X_{r}+X_{n}\right]$$

  Prove that the optimal policy may be expressed in terms of the numbers $b_{0}, b_{1}, \ldots$, $b_{n}$ where $b_{n}=1, b_{r}=b_{r+1}+\mathbb{E} \max \left(b_{r+1} W_{r}, 1\right)$, for $r<n$, and determine the optimal expected total consumption.

  comment

• A4.12 B4.16

  Stochastic Financial Models

  Part II, 2002

  Write an essay on the Black-Scholes formula for the price of a European call option on a stock. Your account should include a derivation of the formula and a careful analysis of its dependence on the parameters of the model.

  comment

• A1.11 B1.16

  Stochastic Financial Models

  Part II, 2003

  (i) In the context of a single-period financial market with $d$ traded assets, what is an arbitrage? What is an equivalent martingale measure?

  A simple single-period financial market contains two assets, $S^{0}$ (a bond), and $S^{1}$ (a share). The period can be good, bad, or indifferent, with probabilities $1 / 3$ each. At the beginning of the period, time 0 , both assets are worth 1 , i.e.

  $$S_{0}^{0}=1=S_{0}^{1}$$

  and at the end of the period, time 1 , the share is worth

  $$S_{1}^{1}= \begin{cases}a & \text { if the period was bad, } \\ b & \text { if the period was indifferent } \\ c & \text { if the period was good }\end{cases}$$

  where $a<b<c$. The bond is always worth 1 at the end of the period. Show that there is no arbitrage in this market if and only if $a<1<c$.

  (ii) An agent with $C^{2}$ strictly increasing strictly concave utility $U$ has wealth $w_{0}$ at time 0 , and wishes to invest his wealth in shares and bonds so as to maximise his expected utility of wealth at time 1 . Explain how the solution to his optimisation problem generates an equivalent martingale measure.

  Assume now that $a=3 / 4, b=1$, and $c=3 / 2$. Characterise all equivalent martingale measures for this problem. Characterise all equivalent martingale measures which arise as solutions of an agent's optimisation problem.

  Calculate the largest and smallest possible prices for a European call option with strike 1 and expiry 1, as the pricing measure ranges over all equivalent martingale measures. Calculate the corresponding bounds when the pricing measure is restricted to the set arising from expected-utility-maximising agents' optimisation problems.

  comment

• A3.11 B3.16

  Stochastic Financial Models

  Part II, 2003

  (i) What does it mean to say that the process $\left(W_{t}\right)_{t \geqslant 0}$ is a Brownian motion? What does it mean to say that the process $\left(M_{t}\right)_{t \geqslant 0}$ is a martingale?

  Suppose that $\left(W_{t}\right)_{t \geqslant 0}$ is a Brownian motion and the process $\left(X_{t}\right)_{t \geqslant 0}$ is given in terms of $W$ as

  $$X_{t}=x_{0}+\sigma W_{t}+\mu t$$

  for constants $\sigma, \mu$. For what values of $\theta$ is the process

  $$M_{t}=\exp \left(\theta X_{t}-\lambda t\right)$$

  a martingale? (Here, $\lambda$ is a positive constant.)

  (ii) In a standard Black-Scholes model, the price at time $t$ of a share is represented as $S_{t}=\exp \left(X_{t}\right)$. You hold a perpetual American put option on this share, with strike $K$; you may exercise at any stopping time $\tau$, and upon exercise you receive $\max \left\{0, K-S_{\tau}\right\}$. Let $0<a<\log K$. Suppose you plan to use the exercise policy: 'Exercise as soon as the price falls to $e^{a}$ or lower.' Calculate what the option would be worth if you were to follow this policy. (Assume that the riskless rate of interest is constant and equal to $r>0$.) For what choice of $a$ is this value maximised?

  comment

• A4.12 B4.16

  Stochastic Financial Models

  Part II, 2003

  A single-period market contains $d$ risky assets, $S^{1}, S^{2}, \ldots, S^{d}$, initially worth $\left(S_{0}^{1}, S_{0}^{2}, \ldots, S_{0}^{d}\right)$, and at time 1 worth random amounts $\left(S_{1}^{1}, S_{1}^{2}, \ldots, S_{1}^{d}\right)$ whose first two moments are given by

  $$\mu=E S_{1}, \quad V=\operatorname{cov}\left(S_{1}\right) \equiv E\left[\left(S_{1}-E S_{1}\right)\left(S_{1}-E S_{1}\right)^{T}\right]$$

  An agent with given initial wealth $w_{0}$ is considering how to invest in the available assets, and has asked for your advice. Develop the theory of the mean-variance efficient frontier far enough to exhibit explicitly the minimum-variance portfolio achieving a required mean return, assuming that $V$ is non-singular. How does your analysis change if a riskless asset $S^{0}$ is added to the market? Under what (sufficient) conditions would an agent maximising expected utility actually choose a portfolio on the mean-variance efficient frontier?

  comment

• A1.11 B1.16

  Stochastic Financial Models

  Part II, 2004

  (i) What does it mean to say that $U$ is a utility function? What is a utility function with constant absolute risk aversion (CARA)?

  Let $S_{t} \equiv\left(S_{t}^{1}, \ldots, S_{t}^{d}\right)^{T}$ denote the prices at time $t=0,1$ of $d$ risky assets, and suppose that there is also a riskless zeroth asset, whose price at time 0 is 1 , and whose price at time 1 is $1+r$. Suppose that $S_{1}$ has a multivariate Gaussian distribution, with mean $\mu_{1}$ and non-singular covariance $V$. An agent chooses at time 0 a portfolio $\theta=\left(\theta^{1}, \ldots, \theta^{d}\right)^{T}$ of holdings of the $d$ risky assets, at total cost $\theta \cdot S_{0}$, and at time 1 realises his gain $X=\theta \cdot\left(S_{1}-(1+r) S_{0}\right)$. Given that he wishes the mean of $X$ to be equal to $m$, find the smallest value that the variance $v$ of $X$ can be. What is the portfolio that achieves this smallest variance? Hence sketch the region in the $(v, m)$ plane of pairs $(v, m)$ that can be achieved by some choice of $\theta$, and indicate the mean-variance efficient frontier.

  (ii) Suppose that the agent has a CARA utility with coefficient $\gamma$ of absolute risk aversion. What portfolio will he choose in order to maximise $E U(X)$ ? What then is the mean of $X$ ?

  Regulation requires that the agent's choice of portfolio $\theta$ has to satisfy the valueat-risk (VaR) constraint

  $$m \geqslant-L+a \sqrt{v},$$

  where $L>0$ and $a>0$ are determined by the regulatory authority. Show that this constraint has no effect on the agent's decision if $\kappa \equiv \sqrt{\mu \cdot V^{-1} \mu} \geqslant a$. If $\kappa<a$, will this constraint necessarily affect the agent's choice of portfolio?

  comment

• A3.11 B3.16

  Stochastic Financial Models

  Part II, 2004

  (i) Consider a single-period binomial model of a riskless asset (asset 0 ), worth 1 at time 0 and $1+r$ at time 1 , and a risky asset (asset 1 ), worth 1 at time 0 and worth $u$ at time 1 if the period was good, otherwise worth $d$. Assuming that

  $$d<1+r<u$$

  show how any contingent claim $Y$ to be paid at time 1 can be priced and exactly replicated. Briefly explain the significance of the condition $(*)$, and indicate how the analysis of the single-period model extends to many periods.

  (ii) Now suppose that $u=5 / 3, d=2 / 3, r=1 / 3$, and that the risky asset is worth $S_{0}=864=2^{5} \times 3^{3}$ at time zero. Show that the time- 0 value of an American put option with strike $K=S_{0}$ and expiry at time $t=3$ is equal to 79 , and find the optimal exercise policy.

  comment

• A4.12 B4.16

  Stochastic Financial Models

  Part II, 2004

  What is Brownian motion $\left(B_{t}\right)_{t \geqslant 0}$ ? Briefly explain how Brownian motion can be considered as a limit of simple random walks. State the Reflection Principle for Brownian motion, and use it to derive the distribution of the first passage time $\tau_{a} \equiv \inf \left\{t: B_{t}=a\right\}$ to some level $a>0$.

  Suppose that $X_{t}=B_{t}+c t$, where $c>0$ is constant. Stating clearly any results to which you appeal, derive the distribution of the first-passage time $\tau_{a}^{(c)} \equiv \inf \left\{t: X_{t}=a\right\}$ to $a>0$.

  Now let $\sigma_{a} \equiv \sup \left\{t: X_{t}=a\right\}$, where $a>0$. Find the density of $\sigma_{a}$.

  comment

• 1.II.28J

  Stochastic Financial Models

  Part II, 2005

  Let $X \equiv\left(X_{0}, X_{1}, \ldots, X_{J}\right)^{T}$ be a zero-mean Gaussian vector, with covariance matrix $V=\left(v_{j k}\right)$. In a simple single-period economy with $J$ agents, agent $i$ will receive $X_{i}$ at time $1(i=1, \ldots, J)$. If $Y$ is a contingent claim to be paid at time 1 , define agent $i$ 's reservation bid price for $Y$, assuming his preferences are given by $E\left[U_{i}\left(X_{i}+Z\right)\right]$ for any contingent claim $Z$.

  Assuming that $U_{i}(x) \equiv-\exp \left(-\gamma_{i} x\right)$ for each $i$, where $\gamma_{i}>0$, show that agent $i$ 's reservation bid price for $\lambda$ units of $X_{0}$ is

  $$p_{i}(\lambda)=-\frac{1}{2} \gamma_{i}\left(\lambda^{2} v_{00}+2 \lambda v_{0 i}\right)$$

  As $\lambda \rightarrow 0$, find the limit of agent $i$ 's per-unit reservation bid price for $X_{0}$, and comment on the expression you obtain.

  The agents bargain, and reach an equilibrium. Assuming that the contingent claim $X_{0}$ is in zero net supply, show that the equilibrium price of $X_{0}$ will be

  $$p=-\Gamma v_{0 \bullet}$$

  where $\Gamma^{-1}=\sum_{i=1}^{J} \gamma_{i}^{-1}$ and $v_{0 \bullet}=\sum_{i=1}^{J} v_{0 i}$. Show that at that price agent $i$ will choose to buy

  $$\theta_{i}=\left(\Gamma v_{0 \bullet}-\gamma_{i} v_{0 i}\right) /\left(\gamma_{i} v_{00}\right)$$

  units of $X_{0}$.

  By computing the improvement in agent $i$ 's expected utility, show that the value to agent $i$ of access to this market is equal to a fixed payment of

  $$\frac{\left(\gamma_{i} v_{0 i}-\Gamma v_{0 \bullet}\right)^{2}}{2 \gamma_{i} v_{00}}$$

  comment

• 2.II.28J

  Stochastic Financial Models

  Part II, 2005

  (i) At the beginning of year $n$, an investor makes decisions about his investment and consumption for the coming year. He first takes out an amount $c_{n}$ from his current wealth $w_{n}$, and sets this aside for consumption. He splits his remaining wealth between a bank account (unit wealth invested at the start of the year will have grown to a sure amount $r>1$ by the end of the year), and the stock market. Unit wealth invested in the stock market will have become the random amount $X_{n+1}>0$ by the end of the year.

  The investor's objective is to invest and consume so as to maximise the expected value of $\sum_{n=1}^{N} U\left(c_{n}\right)$, where $U$ is strictly increasing and strictly convex. Consider the dynamic programming equation (Bellman equation) for his problem,

  $$\begin{aligned} V_{n}(w) &=\sup _{c, \theta}\left\{U(c)+E_{n}\left[V_{n+1}\left(\theta(w-c) X_{n+1}+(1-\theta)(w-c) r\right)\right]\right\} \quad(0 \leqslant n<N), \\ V_{N}(w) &=U(w) . \end{aligned}$$

  Explain all undefined notation, and explain briefly why the equation holds.

  (ii) Supposing that the $X_{i}$ are independent and identically distributed, and that $U(x)=x^{1-R} /(1-R)$, where $R>0$ is different from 1 , find as explicitly as you can the form of the agent's optimal policy.

  (iii) Return to the general problem of (i). Assuming that the sample space $\Omega$ is finite, and that all suprema are attained, show that

  $$\begin{aligned} E_{n}\left[V_{n+1}^{\prime}\left(w_{n+1}^{*}\right)\left(X_{n+1}-r\right)\right] &=0 \\ r E_{n}\left[V_{n+1}^{\prime}\left(w_{n+1}^{*}\right)\right] &=U^{\prime}\left(c_{n}^{*}\right) \\ r E_{n}\left[V_{n+1}^{\prime}\left(w_{n+1}^{*}\right)\right] &=V_{n}^{\prime}\left(w_{n}^{*}\right) \end{aligned}$$

  where $\left(c_{n}^{*}, w_{n}^{*}\right)_{0 \leqslant n \leqslant N}$ denotes the optimal consumption and wealth process for the problem. Explain the significance of each of these equalities.

  comment

• 3.II.27J

  Stochastic Financial Models

  Part II, 2005

  Suppose that over two periods a stock price moves on a binomial tree:

  

  (a) Find an arbitrage opportunity when the riskless rate equals $1 / 10$. Give precise details of when and how much you buy, borrow and sell.

  (b) From here on, assume instead that the riskless rate equals $1 / 4$. Determine the equivalent martingale measure. [No proof is required.]

  (c) Determine the time-zero price of an American put with strike 15 and expiry 2 . Assume you sell it at this price. Which hedge do you put on at time zero? Consider the scenario of two bad periods. How does your hedge work?

  (d) The buyer of the American put turns out to be an unsophisticated investor who fails to use his early exercise right when he should. Assume the first period was bad. How much profit can you make out of this? You should detail your exact strategy.

  comment

• 4.II.28J

  Stochastic Financial Models

  Part II, 2005

  (a) In the context of the Black-Scholes formula, let $S_{0}$ be spot price, $K$ be strike price, $T$ be time to maturity, and assume constant interest rate $r$, volatility $\sigma$ and absence of dividends. Write down explicitly the prices of a European call and put,

  $$E C\left(S_{0}, K, \sigma, r, T\right) \text { and } E P\left(S_{0}, K, \sigma, r, T\right)$$

  Use $\Phi$ for the normal distribution function. [No proof is required.]

  (b) From here on assume $r=0$. Keeping $T, \sigma$ fixed, we shorten the notation to $E C\left(S_{0}, K\right)$ and similarly for $E P$. Show that put-call symmetry holds:

  $$E C\left(S_{0}, K\right)=E P\left(K, S_{0}\right)$$

  Check homogeneity: for every real $\alpha>0$

  $$E C\left(\alpha S_{0}, \alpha K\right)=\alpha E C\left(S_{0}, K\right)$$

  (c) Show that the price of a down-and-out European call with strike $K<S_{0}$ and barrier $B \leqslant K$ is given by

  $$E C\left(S_{0}, K\right)-\frac{S_{0}}{B} E C\left(\frac{B^{2}}{S_{0}}, K\right)$$

  (d)

  (i) Specialize the last expression to $B=K$ and simplify.

  (ii) Answer a popular interview question in investment banks: What is the fair value of a down-and-out call given that $S_{0}=100, B=K=80, \sigma=20 \%, r=0, T=1$ ? Identify the corresponding hedge. [It may be helpful to compute Delta first.]

  (iii) Does this hedge work beyond the Black-Scholes model? When does it fail?

  comment

• 1.II.28I

  Stochastic Financial Models

  Part II, 2006

  Over two periods a stock price $\left\{S_{t}: t=0,1,2\right\}$ moves on a binomial tree.

  

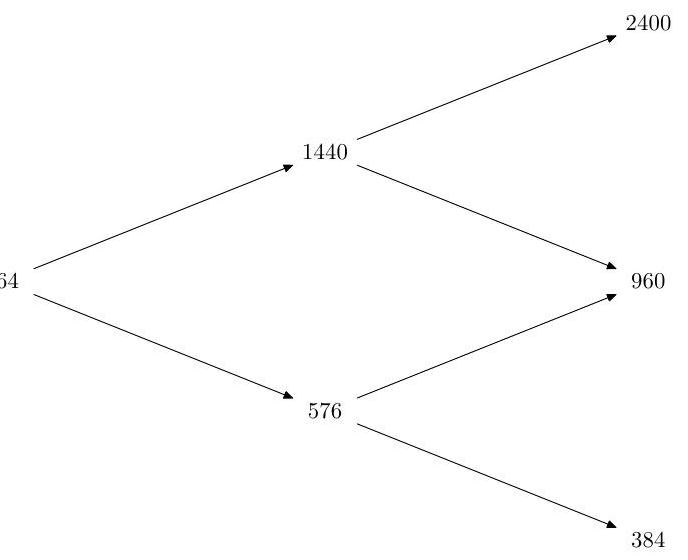
  Assuming that the riskless rate is constant at $r=1 / 3$, verify that all risk-neutral up-probabilities are given by one value $p \in(0,1)$. Find the time- 0 value of the following three put options all struck at $K=S_{0}=864=2^{5} \times 3^{3}$, with expiry 2 :

  (a) a European put;

  (b) an American put;

  (c) a European put modified by raising the strike to $K=992$ at time 1 if the stock went down in the first period.

  comment

• 2.II.28I

  Stochastic Financial Models

  Part II, 2006

  (a) In the context of a single-period financial market with $n$ traded assets and a single riskless asset earning interest at rate $r$, what is an arbitrage? What is an equivalent martingale measure? Explain marginal utility pricing, and how it leads to an equivalent martingale measure.

  (b) Consider the following single-period market with two assets. The first is a riskless bond, worth 1 at time 0 , and 1 at time 1 . The second is a share, worth 1 at time 0 and worth $S_{1}$ at time 1 , where $S_{1}$ is uniformly distributed on the interval $[0, a]$, where $a>0$. Under what condition on $a$ is this model arbitrage free? When it is, characterise the set $\mathcal{E}$ of equivalent martingale measures.

  An agent with $C^{2}$ utility $U$ and with wealth $w$ at time 0 aims to pick the number $\theta$ of shares to hold so as to maximise his expected utility of wealth at time 1 . Show that he will choose $\theta$ to be positive if and only if $a>2$.

  An option pays $\left(S_{1}-1\right)^{+}$at time 1 . Assuming that $a=2$, deduce that the agent's price for this option will be $1 / 4$, and show that the range of possible prices for this option as the pricing measure varies in $\mathcal{E}$ is the interval $\left(0, \frac{1}{2}\right)$.

  comment

• 3.II.27I

  Stochastic Financial Models

  Part II, 2006

  Let $r$ denote the riskless rate and let $\sigma>0$ be a fixed volatility parameter.

  (a) Let $\left(S_{t}\right)_{t \geqslant 0}$ be a Black-Scholes asset with zero dividends:

  $$S_{t}=S_{0} \exp \left(\sigma B_{t}+\left(r-\sigma^{2} / 2\right) t\right),$$

  where $B$ is standard Brownian motion. Derive the Black-Scholes partial differential equation for the price of a European option on $S$ with bounded payoff $\varphi\left(S_{T}\right)$ at expiry $T$ :

  $$\partial_{t} V+\frac{1}{2} \sigma^{2} S^{2} \partial_{S S} V+r S \partial_{S} V-r V=0, \quad V(T, \cdot)=\varphi(\cdot)$$

  [You may use the fact that for $C^{2}$ functions $f: \mathbb{R} \times \mathbb{R} \rightarrow \mathbb{R}$ satisfying exponential growth conditions, and standard Brownian motion $B$, the process

  $$C_{t}^{f}=f\left(t, B_{t}\right)-\int_{0}^{t}\left(\partial_{t} f+\frac{1}{2} \partial_{B B} f\right)\left(s, B_{s}\right) d s$$

  is a martingale.]

  (b) Indicate the changes in your argument when the asset pays dividends continuously at rate $D>0$. Find the corresponding Black-Scholes partial differential equation.

  (c) Assume $D=0$. Find a closed form solution for the time-0 price of a European power option with payoff $S_{T}^{n}$.

  comment

• 4.II.28I

  Stochastic Financial Models

  Part II, 2006

  State the definitions of a martingale and a stopping time.

  State and prove the optional sampling theorem.

  If $\left(M_{n}, \mathcal{F}_{n}\right)_{n \geqslant 0}$ is a martingale, under what conditions is it true that $M_{n}$ converges with probability 1 as $n \rightarrow \infty$ ? Show by an example that some condition is necessary.

  A market consists of $K>1$ agents, each of whom is either optimistic or pessimistic. At each time $n=0,1, \ldots$, one of the agents is selected at random, and chooses to talk to one of the other agents (again selected at random), whose type he then adopts. If choices in different periods are independent, show that the proportion of pessimists is a martingale. What can you say about the limiting behaviour of the proportion of pessimists as time $n$ tends to infinity?

  comment

• 1.II.28J

  Stochastic Financial Models

  Part II, 2007

  (i) What does it mean to say that a process $\left(M_{t}\right)_{t \geqslant 0}$ is a martingale? What does the martingale convergence theorem tell us when applied to positive martingales?

  (ii) What does it mean to say that a process $\left(B_{t}\right)_{t \geqslant 0}$ is a Brownian motion? Show that $\sup _{t \geqslant 0} B_{t}=\infty$ with probability one.

  (iii) Suppose that $\left(B_{t}\right)_{t \geqslant 0}$ is a Brownian motion. Find $\mu$ such that

  $$S_{t}=\exp \left(x_{0}+\sigma B_{t}+\mu t\right)$$

  is a martingale. Discuss the limiting behaviour of $S_{t}$ and $\mathbb{E}\left(S_{t}\right)$ for this $\mu$ as $t \rightarrow \infty$.

  comment

• 2.II.28J

  Stochastic Financial Models

  Part II, 2007

  In the context of a single-period financial market with $n$ traded assets, what is an arbitrage? What is an equivalent martingale measure?

  Fix $\epsilon \in(0,1)$ and consider the following single-period market with 3 assets:

  Asset 1 is a riskless bond and pays no interest.

  Asset 2 is a stock with initial price $£ 1$ per share; its possible final prices are $u=1+\epsilon$ with probability $3 / 5$ and $d=1-\epsilon$ with probability $2 / 5$.

  Asset 3 is another stock that behaves like an independent copy of asset 2 .

  Find all equivalent martingale measures for the problem and characterise all contingent claims that can be replicated.

  Consider a contingent claim $Y$ that pays 1 if both risky assets move in the same direction and zero otherwise. Show that the lower arbitrage bound, simply obtained by calculating all possible prices as the pricing measure ranges over all equivalent martingale measures, is zero. Why might someone pay for such a contract?

  comment

• 3.II.27J

  Stochastic Financial Models

  Part II, 2007

  Suppose that over two periods a stock price moves on a binomial tree

  

  (i) Determine for what values of the riskless rate $r$ there is no arbitrage. From here on, fix $r=1 / 4$ and determine the equivalent martingale measure.

  (ii) Find the time-zero price and replicating portfolio for a European put option with strike 15 and expiry $2 .$

  (iii) Find the time-zero price and optimal exercise policy for an American put option with the same strike and expiry.

  (iv) Deduce the corresponding (European and American) call option prices for the same strike and expiry.

  comment

• 4.II.28J

  Stochastic Financial Models

  Part II, 2007

  Briefly describe the Black-Scholes model. Consider a "cash-or-nothing" option with strike price $K$, i.e. an option whose payoff at maturity is

  $$f\left(S_{T}\right)= \begin{cases}1 & \text { if } \quad S_{T}>K \\ 0 & \text { if } \quad S_{T} \leqslant K\end{cases}$$

  It can be interpreted as a bet that the stock will be worth at least $K$ at time $T$. Find a formula for its value at time $t$, in terms of the spot price $S_{t}$. Find a formula for its Delta (i.e. its hedge ratio). How does the Delta behave as $t \rightarrow T$ ? Why is it difficult, in practice, to hedge such an instrument?

  comment

• 1.II.28J

  Stochastic Financial Models

  Part II, 2008

  (a) In the context of the Black-Scholes formula, let $S_{0}$ be the time- 0 spot price, $K$ be the strike price, $T$ be the time to maturity, and let $\sigma$ be the volatility. Assume that the interest rate $r$ is constant and assume absence of dividends. Write $\mathrm{EC}\left(S_{0}, K, \sigma, r, T\right)$ for the time- 0 price of a standard European call. The Black-Scholes formula can be written in the following form

  $$\operatorname{EC}\left(S_{0}, K, \sigma, r, T\right)=S_{0} \Phi\left(d_{1}\right)-e^{-r T} K \Phi\left(d_{2}\right)$$

  State how the quantities $d_{1}$ and $d_{2}$ depend on $S_{0}, K, \sigma, r$ and $T$.

  Assume that you sell this option at time 0 . What is your replicating portfolio at time 0 ?

  [No proofs are required.]

  (b) Compute the limit of $\operatorname{EC}\left(S_{0}, K, \sigma, r, T\right)$ as $\sigma \rightarrow \infty$. Construct an explicit arbitrage under the assumption that European calls are traded above this limiting price.

  (c) Compute the limit of $\operatorname{EC}\left(S_{0}, K, \sigma, r, T\right)$ as $\sigma \rightarrow 0$. Construct an explicit arbitrage under the assumption that European calls are traded below this limiting price.

  (d) Express in terms of $S_{0}, d_{1}$ and $T$ the derivative

  $$\frac{\partial}{\partial \sigma} \operatorname{EC}\left(S_{0}, K, \sigma, r, T\right)$$

  [Hint: you may find it useful to express $\frac{\partial}{\partial \sigma} d_{1}$ in terms of $\frac{\partial}{\partial \sigma} d_{2}$.]

  [You may use without proof the formula $S_{0} \Phi^{\prime}\left(d_{1}\right)-e^{-r T} K \Phi^{\prime}\left(d_{2}\right)=0$.]

  (e) Say what is meant by implied volatility and explain why the previous results make it well-defined.

  comment

• 2.II.28J

  Stochastic Financial Models

  Part II, 2008

  (a) Let $\left(B_{t}: t \geqslant 0\right)$ be a Brownian motion and consider the process

  $$Y_{t}=Y_{0} e^{\sigma B_{t}+\left(\mu-\frac{1}{2} \sigma^{2}\right) t}$$

  for $Y_{0}>0$ deterministic. For which values of $\mu$ is $\left(Y_{t}: t \geqslant 0\right)$ a supermartingale? For which values of $\mu$ is $\left(Y_{t}: t \geqslant 0\right)$ a martingale? For which values of $\mu$ is $\left(1 / Y_{t}: t \geqslant 0\right)$ a martingale? Justify your answers.

  (b) Assume that the riskless rates of return for Dollar investors and Euro investors are $r_{D}$ and $r_{E}$ respectively. Thus, 1 Dollar at time 0 in the bank account of a Dollar investor will grow to $e^{r_{D} t}$ Dollars at time $t$. For a Euro investor, the Dollar is a risky, tradable asset. Let $\mathbb{Q}_{E}$ be his equivalent martingale measure and assume that the EUR/USD exchange rate at time $t$, that is, the number of Euros that one Dollar will buy at time $t$, is given by

  $$Y_{t}=Y_{0} e^{\sigma B_{t}+\left(\mu-\frac{1}{2} \sigma^{2}\right) t},$$

  where $\left(B_{t}\right)$ is a Brownian motion under $\mathbb{Q}_{E}$. Determine $\mu$ as function of $r_{D}$ and $r_{E}$. Verify that $Y$ is a martingale if $r_{D}=r_{E}$.

  (c) Let $r_{D}, r_{E}$ be as in part (b). Let now $\mathbb{Q}_{D}$ be an equivalent martingale measure for a Dollar investor and assume that the EUR/USD exchange rate at time $t$ is given by

  $$Y_{t}=Y_{0} e^{\sigma B_{t}+\left(\mu-\frac{1}{2} \sigma^{2}\right) t}$$

  where now $\left(B_{t}\right)$ is a Brownian motion under $\mathbb{Q}_{D}$. Determine $\mu$ as function of $r_{D}$ and $r_{E}$. Given $r_{D}=r_{E}$, check, under $\mathbb{Q}_{D}$, that is $Y$ is not a martingale but that $1 / Y$ is a martingale.

  (d) Assuming still that $r_{D}=r_{E}$, rederive the final conclusion of part (c), namely the martingale property of $1 / Y$, directly from part (b).

  comment

• 3.II.27J

  Stochastic Financial Models

  Part II, 2008

  Consider a vector of asset prices evolving over time $\bar{S}=\left(S_{t}^{0}, S_{t}^{1}, \ldots, S_{t}^{d}\right)_{t \in\{0,1, \ldots, T\}}$. The asset price $S^{0}$ is assumed constant over time. In this context, explain what is an arbitrage and prove that the existence of an equivalent martingale measure implies noarbitrage.

  Suppose that over two periods a stock price moves on a binomial tree

  

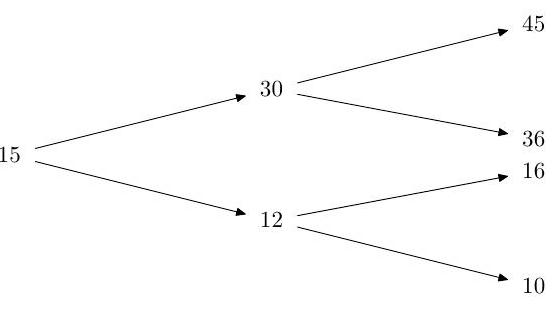
  Assume riskless rate $r=1 / 4$. Determine the equivalent martingale measure. [No proof is required.]

  Sell an American put with strike 15 and expiry 2 at its no-arbitrage price, which you should determine.

  Verify that the buyer of the option should use his early exercise right if the first period is bad.

  Assume that the first period is bad, and that the buyer forgets to exercise. How much risk-free profit can you lock in?

  comment

• 4.II.28J

  Stochastic Financial Models

  Part II, 2008

  (a) Consider a family $\left(X_{n}: n \geqslant 0\right)$ of independent, identically distributed, positive random variables and fix $z_{0}>0$. Define inductively

  $$z_{n+1}=z_{n} X_{n}, \quad n \geqslant 0$$

  Compute, for $n \in\{1, \ldots, N\}$, the conditional expectation $\mathbb{E}\left(z_{N} \mid z_{n}\right)$.

  (b) Fix $R \in[0,1)$. In the setting of part (a), compute also $\mathbb{E}\left(U\left(z_{N}\right) \mid z_{n}\right)$, where

  $$U(x)=x^{1-R} /(1-R), \quad x \geqslant 0 .$$

  (c) Let $U$ be as in part (b). An investor with wealth $w_{0}>0$ at time 0 wishes to invest it in such a way as to maximise $\mathbb{E}\left(U\left(w_{N}\right)\right)$ where $w_{N}$ is the wealth at the start of day $N$. Let $\alpha \in[0,1]$ be fixed. On day $n$, he chooses the proportion $\theta \in[\alpha, 1]$ of his wealth to invest in a single risky asset, so that his wealth at the start of day $n+1$ will be

  $$w_{n+1}=w_{n}\left\{\theta X_{n}+(1-\theta)(1+r)\right\}$$

  Here, $\left(X_{n}: n \geqslant 0\right)$ is as in part (a) and $r$ is the per-period riskless rate of interest. If $V_{n}(w)=\sup \mathbb{E}\left(U\left(w_{N}\right) \mid w_{n}=w\right)$ denotes the value function of this optimization problem, show that $V_{n}\left(w_{n}\right)=a_{n} U\left(w_{n}\right)$ and give a formula for $a_{n}$. Verify that, in the case $\alpha=1$, your answer is in agreement with part (b).

  comment

• Paper 3, Section II, J

  Stochastic Financial Models

  Part II, 2009

  What is a Brownian motion? State the assumptions of the Black-Scholes model of an asset price, and derive the time- 0 price of a European call option struck at $K$, and expiring at $T$.

  Find the time- 0 price of a European call option expiring at $T$, but struck at $S_{t}$, where $t \in(0, T)$, and $S_{t}$ is the price of the underlying asset at time $t$.

  comment

• Paper 1, Section II, J

  Stochastic Financial Models

  Part II, 2009

  An investor must decide how to invest his initial wealth $w_{0}$ in $n$ assets for the coming year. At the end of the year, one unit of asset $i$ will be worth $X_{i}, i=1, \ldots, n$, where $X=\left(X_{1}, \ldots, X_{n}\right)^{T}$ has a multivariate normal distribution with mean $\mu$ and non-singular covariance matrix $V$. At the beginning of the year, one unit of asset $i$ costs $p_{i}$. In addition, he may invest in a riskless bank account; an initial investment of 1 in the bank account will have grown to $1+r>1$ at the end of the year.

  (a) The investor chooses to hold $\theta_{i}$ units of asset $i$, with the remaining $\varphi=w_{0}-\theta \cdot p$ in the bank account. His objective is to minimise the variance of his wealth $w_{1}=\varphi(1+r)+\theta \cdot X$ at the end of the year, subject to a required mean value $m$ for $w_{1}$. Derive the optimal portfolio $\theta^{*}$, and the minimised variance.

  (b) Describe the set $A \subseteq \mathbb{R}^{2}$ of achievable pairs $\left(\mathbb{E}\left[w_{1}\right], \operatorname{var}\left(w_{1}\right)\right)$ of mean and variance of the terminal wealth. Explain what is meant by the mean-variance efficient frontier as you do so.

  (c) Suppose that the investor requires expected mean wealth at time 1 to be $m$. He wishes to minimise the expected shortfall $\mathbb{E}\left[\left(w_{1}-(1+r) w_{0}\right)^{-}\right]$subject to this requirement. Show that he will choose a portfolio corresponding to a point on the mean-variance efficient frontier.

  comment

• Paper 4, Section II, J

  Stochastic Financial Models

  Part II, 2009

  An agent with utility $U(x)=-\exp (-\gamma x)$, where $\gamma>0$ is a constant, may select at time 0 a portfolio of $n$ assets, which he then holds to time 1 . The values $X=\left(X_{1}, \ldots, X_{n}\right)^{T}$ of the assets at time 1 have a multivariate normal distribution with mean $\mu$ and nonsingular covariance matrix $V$. Prove that the agent will prefer portfolio $\psi \in \mathbb{R}^{n}$ to portfolio $\theta \in \mathbb{R}^{n}$ if and only if $q(\psi)>q(\theta)$, where

  $$q(x)=x \cdot \mu-\frac{\gamma}{2} x \cdot V x$$

  Determine his optimal portfolio.

  The agent initially holds portfolio $\theta$, which he may change to portfolio $\theta+z$ at cost $\varepsilon \sum_{i=1}^{n}\left|z_{i}\right|$, where $\varepsilon$ is some positive transaction cost. By considering the function $t \mapsto q(\theta+t z)$ for $0 \leqslant t \leqslant 1$, or otherwise, prove that the agent will have no reason to change his initial portfolio $\theta$ if and only if, for every $i=1, \ldots, n$,

  $$\left|\mu_{i}-\gamma(V \theta)_{i}\right| \leqslant \varepsilon$$

  comment

• Paper 2, Section II, J

  Stochastic Financial Models

  Part II, 2009

  What is a martingale? What is a stopping time? State and prove the optional sampling theorem.

  Suppose that $\xi_{i}$ are independent random variables with values in $\{-1,1\}$ and common distribution $\mathbb{P}(\xi=1)=p=1-q$. Assume that $p>q$. Let $S_{n}$ be the random walk such that $S_{0}=0, S_{n}=S_{n-1}+\xi_{n}$ for $n \geqslant 1$. For $z \in(0,1)$, determine the set of values of $\theta$ for which the process $M_{n}=\theta^{S_{n}} z^{n}$ is a martingale. Hence derive the probability generating function of the random time

  $$\tau_{k}=\inf \left\{t: S_{t}=k\right\}$$

  where $k$ is a positive integer. Hence find the mean of $\tau_{k}$.

  Let $\tau_{k}^{\prime}=\inf \left\{t>\tau_{k}: S_{t}=k\right\}$. Clearly the mean of $\tau_{k}^{\prime}$ is greater than the mean of $\tau_{k}$; identify the point in your derivation of the mean of $\tau_{k}$ where the argument fails if $\tau_{k}$ is replaced by $\tau_{k}^{\prime}$.

  comment

• Paper 1, Section II, I

  Stochastic Financial Models

  Part II, 2010

  What is a Brownian motion? State the reflection principle for Brownian motion.

  Let $W=\left(W_{t}\right)_{t \geqslant 0}$ be a Brownian motion. Let $M=\max _{0 \leqslant t \leqslant 1} W_{t}$. Prove

  $$\mathbb{P}\left(M \geqslant x, W_{1} \leqslant x-y\right)=\mathbb{P}\left(M \geqslant x, W_{1} \geqslant x+y\right)$$

  for all $x, y \geqslant 0$. Hence, show that the random variables $M$ and $\left|W_{1}\right|$ have the same distribution.

  Find the density function of the random variable $R=W_{1} / M$.

  comment

• Paper 2, Section II, I

  Stochastic Financial Models

  Part II, 2010

  What is a martingale? What is a supermartingale? What is a stopping time?

  Let $M=\left(M_{n}\right)_{n \geqslant 0}$ be a martingale and $\hat{M}=\left(\hat{M}_{n}\right)_{n \geqslant 0}$ a supermartingale with respect to a common filtration. If $M_{0}=\hat{M}_{0}$, show that $\mathbb{E} M_{T} \geqslant \mathbb{E} \hat{M}_{T}$ for any bounded stopping time $T$.

  [If you use a general result about supermartingales, you must prove it.]

  Consider a market with one stock with prices $S=\left(S_{n}\right)_{n \geqslant 0}$ and constant interest rate $r$. Explain why an investor's wealth $X$ satisfies

  $$X_{n}=(1+r) X_{n-1}+\pi_{n}\left[S_{n}-(1+r) S_{n-1}\right]$$

  where $\pi_{n}$ is the number of shares of the stock held during the $n$th period.

  Given an initial wealth $X_{0}$, an investor seeks to maximize $\mathbb{E} U\left(X_{N}\right)$ where $U$ is a given utility function. Suppose the stock price is such that $S_{n}=S_{n-1} \xi_{n}$ where $\left(\xi_{n}\right)_{n} \geqslant 1$ is a sequence of independent and identically distributed random variables. Let $V$ be defined inductively by

  $$V(n, x, s)=\sup _{p \in \mathbb{R}} \mathbb{E} V\left[n+1,(1+r) x-p s\left(1+r-\xi_{1}\right), s \xi_{1}\right]$$

  with terminal condition $V(N, x, s)=U(x)$ for all $x, s \in \mathbb{R}$.

  Show that the process $\left(V\left(n, X_{n}, S_{n}\right)\right)_{0 \leqslant n \leqslant N}$ is a supermartingale for any trading strategy $\pi$.

  Suppose $\pi^{*}$ is a trading strategy such that the corresponding wealth process $X^{*}$ makes $\left(V\left(n, X_{n}^{*}, S_{n}\right)\right)_{0} \leqslant n \leqslant N$ a martingale. Show that $\pi^{*}$ is optimal.

  comment

• Paper 3, Section II, I

  Stochastic Financial Models

  Part II, 2010

  Consider a market with two assets, a riskless bond and a risky stock, both of whose initial (time-0) prices are $B_{0}=1=S_{0}$. At time 1 , the price of the bond is a constant $B_{1}=R>0$ and the price of the stock $S_{1}$ is uniformly distributed on the interval $[0, C]$ where $C>R$ is a constant.

  Describe the set of state price densities.

  Consider a contingent claim whose payout at time 1 is given by $S_{1}^{2}$. Use the fundamental theorem of asset pricing to show that, if there is no arbitrage, the initial price of the claim is larger than $R$ and smaller than $C$.

  Now consider an investor with initial wealth $X_{0}=1$, and assume $C=3 R$. The investor's goal is to maximize his expected utility of time-1 wealth $\mathbb{E} U\left[R+\pi\left(S_{1}-R\right)\right]$, where $U(x)=\sqrt{x}$. Show that the optimal number of shares of stock to hold is $\pi^{*}=1$.

  What would be the investor's marginal utility price of the contingent claim described above?

  comment

• Paper 4, Section II, I

  Stochastic Financial Models

  Part II, 2010

  Consider a market with no riskless asset and $d$ risky stocks where the price of stock $i \in\{1, \ldots, d\}$ at time $t \in\{0,1\}$ is denoted $S_{t}^{i}$. We assume the vector $S_{0} \in \mathbb{R}^{d}$ is not random, and we let $\mu=\mathbb{E} S_{1}$ and $V=\mathbb{E}\left[\left(S_{1}-\mu\right)\left(S_{1}-\mu\right)^{T}\right]$. Assume $V$ is not singular.

  Suppose an investor has initial wealth $X_{0}=x$, which he invests in the $d$ stocks so that his wealth at time 1 is $X_{1}=\pi^{T} S_{1}$ for some $\pi \in \mathbb{R}^{d}$. He seeks to minimize the $\operatorname{var}\left(X_{1}\right)$ subject to his budget constraint and the condition that $\mathbb{E} X_{1}=m$ for a given constant $m \in \mathbb{R}$.

  Illustrate this investor's problem by drawing a diagram of the mean-variance efficient frontier. Write down the Lagrangian for the problem. Show that there are two vectors $\pi_{A}$ and $\pi_{B}$ (which do not depend on the constants $x$ and $m$ ) such that the investor's optimal portfolio is a linear combination of $\pi_{A}$ and $\pi_{B}$.

  Another investor with initial wealth $Y_{0}=y$ seeks to maximize $\mathbb{E} U\left(Y_{1}\right)$ his expected utility of time 1 wealth, subject to his budget constraint. Assuming that $S_{1}$ is Gaussian and $U(w)=-e^{-\gamma w}$ for a constant $\gamma>0$, show that the optimal portfolio in this case is also a linear combination of $\pi_{A}$ and $\pi_{B}$.

  [You may use the moment generating function of the Gaussian distribution without derivation.]

  Continue to assume $S_{1}$ is Gaussian, but now assume that $U$ is increasing, concave, and twice differentiable, and that $U, U^{\prime}$ and $U^{\prime \prime}$ are of exponential growth but not necessarily of the form $U(w)=-e^{-\gamma w}$. (Recall that a function $f$ is of exponential growth if $|f(w)| \leqslant a e^{b|w|}$ for some constants positive constants $a, b$.) Prove that the utility maximizing investor still holds a linear combination of $\pi_{A}$ and $\pi_{B}$.

  [You may use the Gaussian integration by parts formula

  $$\mathbb{E}[\nabla f(Z)]=\mathbb{E}[Z f(Z)]$$

  where $Z=\left(Z_{1}, \ldots, Z_{d}\right)^{T}$ is a vector of independent standard normal random variables, and $f$ is differentiable and of exponential growth. You may also interchange integration and differentiation without justification.]

  comment

• Paper 1, Section II, J

  Stochastic Financial Models

  Part II, 2011

  In a one-period market, there are $n$ assets whose prices at time $t$ are given by $S_{t}=\left(S_{t}^{1}, \ldots, S_{t}^{n}\right)^{T}, t=0,1$. The prices $S_{1}$ of the assets at time 1 have a $N(\mu, V)$ distribution, with non-singular covariance $V$, and the prices $S_{0}$ at time 0 are known constants. In addition, there is a bank account giving interest $r$, so that one unit of cash invested at time 0 will be worth $(1+r)$ units of cash at time 1 .

  An agent with initial wealth $w_{0}$ chooses a portfolio $\theta=\left(\theta^{1}, \ldots, \theta^{n}\right)$ of the assets to hold, leaving him with $x=w_{0}-\theta \cdot S_{0}$ in the bank account. His objective is to maximize his expected utility

  $$E\left(-\exp \left[-\gamma\left\{x(1+r)+\theta \cdot S_{1}\right\}\right]\right) \quad(\gamma>0)$$

  Find his optimal portfolio in each of the following three situations:

  (i) $\theta$ is unrestricted;

  (ii) no investment in the bank account is allowed: $x=0$;

  (iii) the initial holdings $x$ of cash must be non-negative.

  For the third problem, show that the optimal initial holdings of cash will be zero if and only if

  $$\frac{S_{0} \cdot(\gamma V)^{-1} \mu-w_{0}}{S_{0} \cdot(\gamma V)^{-1} S_{0}} \geqslant 1+r$$

  comment

• Paper 2, Section II, J

  Stochastic Financial Models

  Part II, 2011

  Consider a symmetric simple random walk $\left(Z_{n}\right)_{n \in \mathbb{Z}^{+}}$taking values in statespace $I=h \mathbb{Z}^{2} \equiv\{(i h, j h): i, j \in \mathbb{Z}\}$, where $h \equiv N^{-1}(N$ an integer $)$. Writing $Z_{n} \equiv\left(X_{n}, Y_{n}\right)$, the transition probabilities are given by

  $$P\left(\Delta Z_{n}=(h, 0)\right)=P\left(\Delta Z_{n}=(0, h)\right)=P\left(\Delta Z_{n}=(-h, 0)\right)=P\left(\Delta Z_{n}=(0,-h)\right)=\frac{1}{4},$$

  where $\Delta Z_{n} \equiv Z_{n}-Z_{n-1}$.

  What does it mean to say that $\left(M_{n}, \mathcal{F}_{n}\right)_{n \in \mathbb{Z}^{+}}$is a martingale? Find a condition on $\theta$ and $\lambda$ such that

  $$M_{n}=\exp \left(\theta X_{n}-\lambda Y_{n}\right)$$

  is a martingale. If $\theta=i \alpha$ for some real $\alpha$, show that $M$ is a martingale if

  $$e^{-\lambda h}=2-\cos (\alpha h)-\sqrt{(2-\cos (\alpha h))^{2}-1}$$

  Suppose that the random walk $Z$ starts at position $(0,1) \equiv(0, N h)$ at time 0 , and suppose that

  $$\tau=\inf \left\{n: Y_{n}=0\right\} .$$

  Stating fully any results to which you appeal, prove that

  $$E \exp \left(i \alpha X_{\tau}\right)=e^{-\lambda}$$

  where $\lambda$ is as given at $(*)$. Deduce that as $N \rightarrow \infty$

  $$E \exp \left(i \alpha X_{\tau}\right) \rightarrow e^{-|\alpha|}$$

  and comment briefly on this result.

  comment

• Paper 3, Section II, J

  Stochastic Financial Models

  Part II, 2011

  First, what is a Brownian motion?

  (i) The price $S_{t}$ of an asset evolving in continuous time is represented as

  $$S_{t}=S_{0} \exp \left(\sigma W_{t}+\mu t\right)$$

  where $W$ is a standard Brownian motion, and $\sigma$ and $\mu$ are constants. If riskless investment in a bank account returns a continuously-compounded rate of interest $r$, derive a formula for the time-0 price of a European call option on the asset $S$ with strike $K$ and expiry $T$. You may use any general results, but should state them clearly.

  (ii) In the same financial market, consider now a derivative which pays

  $$Y=\left\{\exp \left(T^{-1} \int_{0}^{T} \log \left(S_{u}\right) d u\right)-K\right\}^{+}$$

  at time $T$. Find the time-0 price for this derivative. Show that it is less than the price of the European call option which you derived in (i).

  comment

• Paper 4, Section II, J

  Stochastic Financial Models

  Part II, 2011

  In a two-period model, two agents enter a negotiation at time 0 . Agent $j$ knows that he will receive a random payment $X_{j}$ at time $1(j=1,2)$, where the joint distribution of $\left(X_{1}, X_{2}\right)$ is known to both agents, and $X_{1}+X_{2}>0$. At the outcome of the negotiation, there will be an agreed risk transfer random variable $Y$ which agent 1 will pay to agent 2 at time 1 . The objective of agent 1 is to maximize $E U_{1}\left(X_{1}-Y\right)$, and the objective of agent 2 is to maximize $E U_{2}\left(X_{2}+Y\right)$, where the functions $U_{j}$ are strictly increasing, strictly concave, $C^{2}$, and have the properties that

  $$\lim _{x \downarrow 0} U_{j}^{\prime}(x)=+\infty, \quad \lim _{x \uparrow \infty} U_{j}^{\prime}(x)=0$$

  Show that, unless there exists some $\lambda \in(0, \infty)$ such that

  $$\frac{U_{1}^{\prime}\left(X_{1}-Y\right)}{U_{2}^{\prime}\left(X_{2}+Y\right)}=\lambda \quad \text { almost surely }$$

  the risk transfer $Y$ could be altered to the benefit of both agents, and so would not be the conclusion of the negotiation.

  Show that, for given $\lambda>0$, the relation $(*)$ determines a unique risk transfer $Y=Y_{\lambda}$, and that $X_{2}+Y_{\lambda}$ is a function of $X_{1}+X_{2}$.

  comment

• Paper 1, Section II, J

  Stochastic Financial Models

  Part II, 2012

  Consider a multi-period binomial model with a risky asset $\left(S_{0}, \ldots, S_{T}\right)$ and a riskless asset $\left(B_{0}, \ldots, B_{T}\right)$. In each period, the value of the risky asset $S$ is multiplied by $u$ if the period was good, and by $d$ otherwise. The riskless asset is worth $B_{t}=(1+r)^{t}$ at time $0 \leqslant t \leqslant T$, where $r \geqslant 0$.

  (i) Assuming that $T=1$ and that

  $$d<1+r<u$$

  show how any contingent claim to be paid at time 1 can be priced and exactly replicated. Briefly explain the significance of the condition (1), and indicate how the analysis of the single-period model extends to many periods.

  (ii) Now suppose that $T=2$. We assume that $u=2, d=1 / 3, r=1 / 2$, and that the risky asset is worth $S_{0}=27$ at time zero. Find the time- 0 value of an American put option with strike price $K=28$ and expiry at time $T=2$, and find the optimal exercise policy. (Assume that the option cannot be exercised immediately at time zero.)

  comment

• Paper 4, Section II, J

  Stochastic Financial Models

  Part II, 2012

  In a one-period market, there are $n$ risky assets whose returns at time 1 are given by a column vector $R=\left(R^{1}, \ldots, R^{n}\right)^{\prime}$. The return vector $R$ has a multivariate Gaussian distribution with expectation $\mu$ and non-singular covariance matrix $V$. In addition, there is a bank account giving interest $r>0$, so that one unit of cash invested at time 0 in the bank account will be worth $R_{f}=1+r$ units of cash at time 1 .

  An agent with the initial wealth $w$ invests $x=\left(x_{1}, \ldots, x_{n}\right)^{\prime}$ in risky assets and keeps the remainder $x_{0}=w-x \cdot \mathbf{1}$ in the bank account. The return on the agent's portfolio is

  $$Z:=x \cdot R+(w-x \cdot \mathbf{1}) R_{f}$$

  The agent's utility function is $u(Z)=-\exp (-\gamma Z)$, where $\gamma>0$ is a parameter. His objective is to maximize $\mathbb{E}(u(Z))$.

  (i) Find the agent's optimal portfolio and its expected return.

  [Hint. Relate $\mathbb{E}(u(Z))$ to $\mathbb{E}(Z)$ and $\operatorname{Var}(Z) .]$

  (ii) Under which conditions does the optimal portfolio that you found in (i) require borrowing from the bank account?

  (iii) Find the optimal portfolio if it is required that all of the agent's wealth be invested in risky assets.

  comment

• Paper 3, Section II, J

  Stochastic Financial Models

  Part II, 2012

  (i) Let $\mathcal{F}=\left\{\mathcal{F}_{n}\right\}_{n=0}^{\infty}$ be a filtration. Give the definition of a martingale and a stopping time with respect to the filtration $\mathcal{F}$.

  (ii) State Doob's optional stopping theorem. Give an example of a martingale $M$ and a stopping time $T$ such that $\mathbb{E}\left(M_{T}\right) \neq \mathbb{E}\left(M_{0}\right)$.

  (iii) Let $S_{n}$ be a standard random walk on $\mathbb{Z}$, that is, $S_{0}=0, S_{n}=X_{1}+\ldots+X_{n}$, where $X_{i}$ are i.i.d. and $X_{i}=1$ or $-1$ with probability $1 / 2$.

  Let $T_{a}=\inf \left\{n \geqslant 0: S_{n}=a\right\}$ where $a$ is a positive integer. Show that for all $\theta>0$,

  $$\mathbb{E}\left(e^{-\theta T_{a}}\right)=\left(e^{\theta}-\sqrt{e^{2 \theta}-1}\right)^{a} .$$

  Carefully justify all steps in your derivation.

  [Hint. For all $\lambda>0$ find $\theta$ such that $M_{n}=\exp \left(-\theta n+\lambda S_{n}\right)$ is a martingale. You may assume that $T_{a}$ is almost surely finite.]

  Let $T=T_{a} \wedge T_{-a}=\inf \left\{n \geqslant 0:\left|S_{n}\right|=a\right\}$. By introducing a suitable martingale, compute $\mathbb{E}\left(e^{-\theta T}\right)$.

  comment

• Paper 2, Section II, J

  Stochastic Financial Models

  Part II, 2012

  (i) Give the definition of Brownian motion.

  (ii) The price $S_{t}$ of an asset evolving in continuous time is represented as

  $$S_{t}=S_{0} \exp \left(\sigma W_{t}+\mu t\right)$$

  where $\left(W_{t}\right)_{t \geqslant 0}$ is a standard Brownian motion and $\sigma$ and $\mu$ are constants. If riskless investment in a bank account returns a continuously compounded rate of interest $r$, derive the Black-Scholes formula for the time-0 price of a European call option on asset $S$ with strike price $K$ and expiry $T$. [Standard results from the course may be used without proof but must be stated clearly.]

  (iii) In the same financial market, a certain contingent claim $C$ pays $\left(S_{T}\right)^{n}$ at time $T$, where $n \geqslant 1$. Find the closed-form expression for the time- 0 value of this contingent claim.

  Show that for every $s>0$ and $n \geqslant 1$,

  $$s^{n}=n(n-1) \int_{0}^{s} k^{n-2}(s-k) d k .$$

  Using this identity, how would you replicate (at least approximately) the contingent claim $C$ with a portfolio consisting only of European calls?

  comment

• Paper 4, Section II, J

  Stochastic Financial Models

  Part II, 2013

  Let $S_{t}:=\left(S_{t}^{1}, S_{t}^{2}, \ldots, S_{t}^{n}\right)^{\mathrm{T}}$ denote the time- $t$ prices of $n$ risky assets in which an agent may invest, $t=0,1$. He may also invest his money in a bank account, which will return interest at rate $r>0$. At time 0 , he knows $S_{0}$ and $r$, and he knows that $S_{1} \sim N(\mu, V)$. If he chooses at time 0 to invest cash value $\theta_{i}$ in risky asset $i$, express his wealth $w_{1}$ at time 1 in terms of his initial wealth $w_{0}>0$, the choices $\theta:=\left(\theta_{1}, \ldots, \theta_{n}\right)^{\mathrm{T}}$, the value of $S_{1}$, and $r$.

  Suppose that his goal is to minimize the variance of $w_{1}$ subject to the requirement that the mean $E\left(w_{1}\right)$ should be at least $m$, where $m \geqslant(1+r) w_{0}$ is given. What portfolio $\theta$ should he choose to achieve this?

  Suppose instead that his goal is to minimize $E\left(w_{1}^{2}\right)$ subject to the same constraint. Show that his optimal portfolio is unchanged.

  comment

• Paper 3, Section II, J

  Stochastic Financial Models

  Part II, 2013

  Suppose that $\left(\varepsilon_{t}\right)_{t=0,1, \ldots, T}$ is a sequence of independent and identically distributed random variables such that $E \exp \left(z \varepsilon_{1}\right)<\infty$ for all $z \in \mathbb{R}$. Each day, an agent receives an income, the income on day $t$ being $\varepsilon_{t}$. After receiving this income, his wealth is $w_{t}$. From this wealth, he chooses to consume $c_{t}$, and invests the remainder $w_{t}-c_{t}$ in a bank account which pays a daily interest rate of $r>0$. Write down the equation for the evolution of $w_{t}$.

  Suppose we are given constants $\beta \in(0,1), A_{T}, \gamma>0$, and define the functions

  $$U(x)=-\exp (-\gamma x), \quad U_{T}(x)=-A_{T} \exp (-\nu x)$$

  where $\nu:=\gamma r /(1+r)$. The agent's objective is to attain

  $$V_{0}(w):=\sup E\left\{\sum_{t=0}^{T-1} \beta^{t} U\left(c_{t}\right)+\beta^{T} U_{T}\left(w_{T}\right) \mid w_{0}=w\right\},$$

  where the supremum is taken over all adapted sequences $\left(c_{t}\right)$. If the value function is defined for $0 \leqslant n<T$ by

  $$V_{n}(w)=\sup E\left\{\sum_{t=n}^{T-1} \beta^{t-n} U\left(c_{t}\right)+\beta^{T-n} U_{T}\left(w_{T}\right) \mid w_{n}=w\right\}$$

  with $V_{T}=U_{T}$, explain briefly why you expect the $V_{n}$ to satisfy

  $$V_{n}(w)=\sup _{c}\left[U(c)+\beta E\left\{V_{n+1}\left((1+r)(w-c)+\varepsilon_{n+1}\right)\right\}\right]$$

  Show that the solution to $(*)$ has the form

  $$V_{n}(w)=-A_{n} \exp (-\nu w),$$

  for constants $A_{n}$ to be identified. What is the form of the consumption choices that achieve the supremum in $(*)$ ?

  comment

• Paper 1, Section II, 29J

  Stochastic Financial Models

  Part II, 2013

  (i) Suppose that the price $S_{t}$ of an asset at time $t$ is given by

  $$S_{t}=S_{0} \exp \left\{\sigma B_{t}+\left(r-\frac{1}{2} \sigma^{2}\right) t\right\}$$

  where $B$ is a Brownian motion, $S_{0}$ and $\sigma$ are positive constants, and $r$ is the riskless rate of interest, assumed constant. In this model, explain briefly why the time-0 price of a derivative which delivers a bounded random variable $Y$ at time $T$ should be given by $E\left(e^{-r T} Y\right)$. What feature of this model ensures that the price is unique?

  Derive an expression $C\left(S_{0}, K, T, r, \sigma\right)$ for the time- 0 price of a European call option with strike $K$ and expiry $T$. Explain the italicized terms.

  (ii) Suppose now that the price $X_{t}$ of an asset at time $t$ is given by

  $$X_{t}=\sum_{j=1}^{n} w_{j} \exp \left\{\sigma_{j} B_{t}+\left(r-\frac{1}{2} \sigma_{j}^{2}\right) t\right\}$$

  where the $w_{j}$ and $\sigma_{j}$ are positive constants, and the other notation is as in part (i) above. Show that the time-0 price of a European call option with strike $K$ and expiry $T$ written on this asset can be expressed as

  $$\sum_{j=1}^{n} C\left(w_{j}, k_{j}, T, r, \sigma_{j}\right)$$

  where the $k_{j}$ are constants. Explain how the $k_{j}$ are characterized.

  comment

• Paper 2, Section II, J

  Stochastic Financial Models

  Part II, 2013

  What does it mean to say that $\left(Y_{n}, \mathcal{F}_{n}\right)_{n \geqslant 0}$ is a supermartingale?

  State and prove Doob's Upcrossing Inequality for a supermartingale.

  Let $\left(M_{n}, \mathcal{F}_{n}\right)_{n \leqslant 0}$ be a martingale indexed by negative time, that is, for each $n \leqslant 0$, $\mathcal{F}_{n-1} \subseteq \mathcal{F}_{n}, M_{n} \in L^{1}\left(\mathcal{F}_{n}\right)$ and $E\left[M_{n} \mid \mathcal{F}_{n-1}\right]=M_{n-1}$. Using Doob's Upcrossing Inequality, prove that the limit $\lim _{n \rightarrow-\infty} M_{n}$ exists almost surely.

  comment

• Paper 4, Section II, K

  Stochastic Financial Models

  Part II, 2014

  Write down the Black-Scholes partial differential equation (PDE), and explain briefly its relevance to option pricing.

  Show how a change of variables reduces the Black-Scholes PDE to the heat equation:

  $$\begin{aligned} &\frac{\partial f}{\partial t}+\frac{1}{2} \frac{\partial^{2} f}{\partial x^{2}}=0 \text { for all }(t, x) \in[0, T) \times \mathbb{R}, \\ &f(T, x)=\varphi(x) \text { for all } x \in \mathbb{R} \end{aligned}$$

  where $\varphi$ is a given boundary function.

  Consider the following numerical scheme for solving the heat equation on the equally spaced grid $\left(t_{n}, x_{k}\right) \in[0, T] \times \mathbb{R}$ where $t_{n}=n \Delta t$ and $x_{k}=k \Delta x, n=0,1, \ldots, N$ and $k \in \mathbb{Z}$, and $\Delta t=T / N$. We approximate $f\left(t_{n}, x_{k}\right)$ by $f_{k}^{n}$ where

  $$0=\frac{f^{n+1}-f^{n}}{\Delta t}+\theta L f^{n+1}+(1-\theta) L f^{n}, \quad f_{k}^{N}=\varphi\left(x_{k}\right)$$

  and $\theta \in[0,1]$ is a constant and the operator $L$ is the matrix with non-zero entries $L_{k k}=-\frac{1}{(\Delta x)^{2}}$ and $L_{k, k+1}=L_{k, k-1}=\frac{1}{2(\Delta x)^{2}}$. By considering what happens when $\varphi(x)=\exp (i \omega x)$, show that the finite-difference scheme $(*)$ is stable if and only if

  $$1 \geqslant \lambda(2 \theta-1),$$

  where $\lambda \equiv \Delta t /(\Delta x)^{2}$. For what values of $\theta$ is the scheme $(*)$ unconditionally stable?

  comment

• Paper 3, Section II, $29 K$

  Stochastic Financial Models

  Part II, 2014

  Derive the Black-Scholes formula $C\left(S_{0}, K, r, T, \sigma\right)$ for the time- 0 price of a European call option with expiry $T$ and strike $K$ written on an asset with volatility $\sigma$ and time-0 price $S_{0}$, and where $r$ is the riskless rate of interest. Explain what is meant by the delta hedge for this option, and determine it explicitly.

  In terms of the Black-Scholes call option price formula $C$, find the time- 0 price of a forward-starting option, which pays $\left(S_{T}-\lambda S_{t}\right)^{+}$at time $T$, where $0<t<T$ and $\lambda>0$ are given. Find the price of an option which pays $\max \left\{S_{T}, \lambda S_{t}\right\}$ at time $T$. How would this option be hedged?

  comment

• Paper 1, Section II, K

  Stochastic Financial Models

  Part II, 2014

  Suppose that $\bar{S}_{t} \equiv\left(S_{t}^{0}, \ldots, S_{t}^{d}\right)^{T}$ denotes the vector of prices of $d+1$ assets at times $t=0,1, \ldots$, and that $\bar{\theta}_{t} \equiv\left(\theta_{t}^{0}, \ldots, \theta_{t}^{d}\right)^{T}$ denotes the vector of the numbers of the $d+1$ different assets held by an investor from time $t-1$ to time $t$. Assuming that asset 0 is a bank account paying zero interest, that is, $S_{t}^{0}=1$ for all $t \geqslant 0$, explain what is meant by the statement that the portfolio process $\left(\bar{\theta}_{t}\right)_{t \geqslant 0}$ is self-financing. If the portfolio process is self-financing, prove that for any $t>0$

  $$\bar{\theta}_{t} \cdot \bar{S}_{t}-\bar{\theta}_{0} \cdot \bar{S}_{0}=\sum_{j=1}^{t} \theta_{j} \cdot \Delta S_{j}$$

  where $S_{j} \equiv\left(S_{j}^{1}, \ldots, S_{j}^{d}\right)^{T}, \Delta S_{j}=S_{j}-S_{j-1}$, and $\theta_{j} \equiv\left(\theta_{j}^{1}, \ldots, \theta_{j}^{d}\right)^{T}$.

  Suppose now that the $\Delta S_{t}$ are independent with common $N(0, V)$ distribution. Let

  $$F(z)=\inf E\left[\sum_{t \geqslant 1}(1-\beta) \beta^{t}\left\{\left(\bar{\theta}_{t} \cdot \bar{S}_{t}-\bar{\theta}_{0} \cdot \bar{S}_{0}\right)^{2}+\sum_{j=1}^{t}\left|\Delta \theta_{j}\right|^{2}\right\} \mid \theta_{0}=z\right]$$

  where $\beta \in(0,1)$ and the infimum is taken over all self-financing portfolio processes $\left(\bar{\theta}_{t}\right)_{t \geqslant 0}$ with $\theta_{0}^{0}=0$. Explain why $F$ should satisfy the equation

  $$F(z)=\beta \inf _{y}\left[y \cdot V y+|y-z|^{2}+F(y)\right]$$

  If $Q$ is a positive-definite symmetric matrix satisfying the equation

  $$Q=\beta(V+I+Q)^{-1}(V+Q)$$

  show that $(*)$ has a solution of the form $F(z)=z \cdot Q z$.

  comment

• Paper 2, Section II, K

  Stochastic Financial Models

  Part II, 2014

  An agent has expected-utility preferences over his possible wealth at time 1 ; that is, the wealth $Z$ is preferred to wealth $Z^{\prime}$ if and only if $E U(Z) \geqslant E U\left(Z^{\prime}\right)$, where the function $U: \mathbb{R} \rightarrow \mathbb{R}$ is strictly concave and twice continuously differentiable. The agent can trade in a market, with the time-1 value of his portfolio lying in an affine space $\mathcal{A}$ of random variables. Assuming cash can be held between time 0 and time 1 , define the agent's time-0 utility indifference price $\pi(Y)$ for a contingent claim with time-1 value $Y$. Assuming any regularity conditions you may require, prove that the map $Y \mapsto \pi(Y)$ is concave.

  

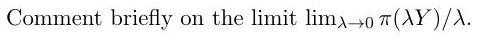
  Consider a market with two claims with time-1 values $X$ and $Y$. Their joint distribution is

  $$\left(\begin{array}{l} X \\ Y \end{array}\right) \sim N\left(\left(\begin{array}{l} \mu_{X} \\ \mu_{Y} \end{array}\right),\left(\begin{array}{ll} V_{X X} & V_{X Y} \\ V_{Y X} & V_{Y Y} \end{array}\right)\right) .$$

  At time 0 , arbitrary quantities of the claim $X$ can be bought at price $p$, but $Y$ is not marketed. Derive an explicit expression for $\pi(Y)$ in the case where

  $$U(x)=-\exp (-\gamma x)$$

  where $\gamma>0$ is a given constant.

  comment

• Paper 4, Section II, $26 \mathrm{~K}$

  Stochastic Financial Models

  Part II, 2015

  (i) An investor in a single-period market with time- 0 wealth $w_{0}$ may generate any time-1 wealth $w_{1}$ of the form $w_{1}=w_{0}+X$, where $X$ is any element of a vector space $V$ of random variables. The investor's objective is to maximize $E\left[U\left(w_{1}\right)\right]$, where $U$ is strictly increasing, concave and $C^{2}$. Define the utility indifference price $\pi(Y)$ of a random variable $Y$.

  Prove that the map $Y \mapsto \pi(Y)$ is concave. [You may assume that any supremum is attained.]

  (ii) Agent $j$ has utility $U_{j}(x)=-\exp \left(-\gamma_{j} x\right), j=1, \ldots, J$. The agents may buy for time- 0 price $p$ a risky asset which will be worth $X$ at time 1 , where $X$ is random and has density

  $$f(x)=\frac{1}{2} \alpha e^{-\alpha|x|}, \quad-\infty<x<\infty .$$

  Assuming zero interest, prove that agent $j$ will optimally choose to buy

  $$\theta_{j}=-\frac{\sqrt{1+p^{2} \alpha^{2}}-1}{\gamma_{j} p}$$

  units of the risky asset at time 0 .

  If the asset is in unit net supply, if $\Gamma^{-1} \equiv \sum_{j} \gamma_{j}^{-1}$, and if $\alpha>\Gamma$, prove that the market for the risky asset will clear at price

  $$p=-\frac{2 \Gamma}{\alpha^{2}-\Gamma^{2}}$$

  What happens if $\alpha \leqslant \Gamma ?$

  comment

• Paper 3, Section II, $26 \mathrm{~K}$

  Stochastic Financial Models

  Part II, 2015

  A single-period market consists of $n$ assets whose prices at time $t$ are denoted by $S_{t}=\left(S_{t}^{1}, \ldots, S_{t}^{n}\right)^{T}, t=0,1$, and a riskless bank account bearing interest rate $r$. The value of $S_{0}$ is given, and $S_{1} \sim N(\mu, V)$. An investor with utility $U(x)=-\exp (-\gamma x)$ wishes to choose a portfolio of the available assets so as to maximize the expected utility of her wealth at time 1. Find her optimal investment.

  What is the market portfolio for this problem? What is the beta of asset $i$ ? Derive the Capital Asset Pricing Model, that

  Excess return of asset $i=$ Excess return of market portfolio $\times \beta_{i}$.

  The Sharpe ratio of a portfolio $\theta$ is defined to be the excess return of the portfolio $\theta$ divided by the standard deviation of the portfolio $\theta$. If $\rho_{i}$ is the correlation of the return on asset $i$ with the return on the market portfolio, prove that

  Sharpe ratio of asset $i=$ Sharpe ratio of market portfolio $\times \rho_{i}$.

  comment

• Paper 1, Section II, $26 K$

  Stochastic Financial Models

  Part II, 2015

  (i) What does it mean to say that $\left(X_{n}, \mathcal{F}_{n}\right)_{n \geqslant 0}$ is a martingale?

  (ii) If $Y$ is an integrable random variable and $Y_{n}=E\left[Y \mid \mathcal{F}_{n}\right]$, prove that $\left(Y_{n}, \mathcal{F}_{n}\right)$ is a martingale. [Standard facts about conditional expectation may be used without proof provided they are clearly stated.] When is it the case that the limit $\lim _{n \rightarrow \infty} Y_{n}$ exists almost surely?

  (iii) An urn contains initially one red ball and one blue ball. A ball is drawn at random and then returned to the urn with a new ball of the other colour. This process is repeated, adding one ball at each stage to the urn. If the number of red balls after $n$ draws and replacements is $X_{n}$, and the number of blue balls is $Y_{n}$, show that $M_{n}=h\left(X_{n}, Y_{n}\right)$ is a martingale, where

  $$h(x, y)=(x-y)(x+y-1)$$

  Does this martingale converge almost surely?

  comment

• Paper 2, Section II, $27 \mathrm{~K}$

  Stochastic Financial Models

  Part II, 2015

  (i) What is Brownian motion?

  (ii) Suppose that $\left(B_{t}\right)_{t \geqslant 0}$ is Brownian motion, and the price $S_{t}$ at time $t$ of a risky asset is given by

  $$S_{t}=S_{0} \exp \left\{\sigma B_{t}+\left(\mu-\frac{1}{2} \sigma^{2}\right) t\right\}$$

  where $\mu>0$ is the constant growth rate, and $\sigma>0$ is the constant volatility of the asset. Assuming that the riskless rate of interest is $r>0$, derive an expression for the price at time 0 of a European call option with strike $K$ and expiry $T$, explaining briefly the basis for your calculation.

  (iii) With the same notation, derive the time-0 price of a European option with expiry $T$ which at expiry pays

  $$\left\{\left(S_{T}-K\right)^{+}\right\}^{2} / S_{T}$$

  comment

• Paper 3, Section II, K

  Stochastic Financial Models

  Part II, 2016

  Consider the following two-period market model. There is a risk-free asset which pays interest at rate $r=1 / 4$. There is also a risky stock with prices $\left(S_{t}\right)_{t \in\{0,1,2\}}$ given by

  

  The above diagram should be read as

  $$\mathbb{P}\left(S_{1}=10 \mid S_{0}=7\right)=2 / 3, \quad \mathbb{P}\left(S_{2}=14 \mid S_{1}=10\right)=1 / 2$$

  and so forth.

  (a) Find the risk-neutral probabilities.

  (b) Consider a European put option with strike $K=10$ expiring at time $T=2$. What is the initial no-arbitrage price of the option? How many shares should be held in each period to replicate the payout?

  (c) Now consider an American put option with the same strike and expiration date. Find the optimal exercise policy, assuming immediate exercise is not allowed. Would your answer change if you were allowed to exercise the option at time 0 ?

  comment

• Paper 4, Section II, K

  Stochastic Financial Models

  Part II, 2016

  Let $U$ be concave and strictly increasing, and let $\mathcal{A}$ be a vector space of random variables. For every random variable $Z$ let

  $$F(Z)=\sup _{X \in \mathcal{A}} \mathbb{E}[U(X+Z)]$$

  and suppose there exists a random variable $X_{Z} \in \mathcal{A}$ such that

  $$F(Z)=\mathbb{E}\left[U\left(X_{Z}+Z\right)\right]$$

  For a random variable $Y$, let $\pi(Y)$ be such that $F(Y-\pi(Y))=F(0)$.

  (a) Show that for every constant $a$ we have $\pi(Y+a)=\pi(Y)+a$, and that if $\mathbb{P}\left(Y_{1} \leqslant Y_{2}\right)=1$, then $\pi\left(Y_{1}\right) \leqslant \pi\left(Y_{2}\right)$. Hence show that if $\mathbb{P}(a \leqslant Y \leqslant b)=1$ for constants $a \leqslant b$, then $a \leqslant \pi(Y) \leqslant b .$

  (b) Show that $Y \mapsto \pi(Y)$ is concave, and hence show $t \mapsto \pi(t Y) / t$ is decreasing for $t>0$.

  (c) Assuming $U$ is continuously differentiable, show that $\pi(t Y) / t$ converges as $t \rightarrow 0$, and that there exists a random variable $X_{0}$ such that

  $$\lim _{t \rightarrow 0} \frac{\pi(t Y)}{t}=\frac{\mathbb{E}\left[U^{\prime}\left(X_{0}\right) Y\right]}{\mathbb{E}\left[U^{\prime}\left(X_{0}\right)\right]}$$

  comment

• Paper 2, Section II, K

  Stochastic Financial Models

  Part II, 2016

  In the context of the Black-Scholes model, let $S_{0}$ be the initial price of the stock, and let $\sigma$ be its volatility. Assume that the risk-free interest rate is zero and the stock pays no dividends. Let $\operatorname{EC}\left(S_{0}, K, \sigma, T\right)$ denote the initial price of a European call option with strike $K$ and maturity date $T$.

  (a) Show that the Black-Scholes formula can be written in the form

  $$\mathrm{EC}\left(S_{0}, K, \sigma, T\right)=S_{0} \Phi\left(d_{1}\right)-K \Phi\left(d_{2}\right)$$

  where $d_{1}$ and $d_{2}$ depend on $S_{0}, K, \sigma$ and $T$, and $\Phi$ is the standard normal distribution function.

  (b) Let $\operatorname{EP}\left(S_{0}, K, \sigma, T\right)$ be the initial price of a put option with strike $K$ and maturity $T$. Show that

  $$\operatorname{EP}\left(S_{0}, K, \sigma, T\right)=\operatorname{EC}\left(S_{0}, K, \sigma, T\right)+K-S_{0}$$

  (c) Show that

  $$\operatorname{EP}\left(S_{0}, K, \sigma, T\right)=\operatorname{EC}\left(K, S_{0}, \sigma, T\right)$$

  (d) Consider a European contingent claim with maturity $T$ and payout

  $$S_{T} I_{\left\{S_{T} \leqslant K\right\}}-K I_{\left\{S_{T}>K\right\}}$$

  Assuming $K>S_{0}$, show that its initial price can be written as $\mathrm{EC}\left(S_{0}, K, \hat{\sigma}, T\right)$ for a volatility parameter $\hat{\sigma}$ which you should express in terms of $S_{0}, K, \sigma$ and $T$.

  comment

• Paper 1, Section II, 28K

  Stochastic Financial Models

  Part II, 2016

  (a) What is a Brownian motion?

  (b) State the Brownian reflection principle. State the Cameron-Martin theorem for Brownian motion with constant drift.

  (c) Let $\left(W_{t}\right)_{t \geqslant 0}$ be a Brownian motion. Show that

  $$\mathbb{P}\left(\max _{0 \leqslant s \leqslant t}\left(W_{s}+a s\right) \leqslant b\right)=\Phi\left(\frac{b-a t}{\sqrt{t}}\right)-e^{2 a b} \Phi\left(\frac{-b-a t}{\sqrt{t}}\right)$$

  where $\Phi$ is the standard normal distribution function.

  (d) Find

  $$\mathbb{P}\left(\max _{u \geqslant t}\left(W_{u}+a u\right) \leqslant b\right)$$

  comment

• Paper 2, Section II, $27 \mathrm{~J}$

  Stochastic Financial Models

  Part II, 2017

  (a) What is a Brownian motion?

  (b) Let $\left(B_{t}, t \geqslant 0\right)$ be a Brownian motion. Show that the process $\tilde{B}_{t}:=\frac{1}{c} B_{c^{2} t}$, $c \in \mathbb{R} \backslash\{0\}$, is also a Brownian motion.

  (c) Let $Z:=\sup _{t \geqslant 0} B_{t}$. Show that $c Z \stackrel{(d)}{=} Z$ for all $c>0$ (i.e. $c Z$ and $Z$ have the same laws). Conclude that $Z \in\{0,+\infty\}$ a.s.

  (d) Show that $\mathbb{P}[Z=+\infty]=1$.

  comment

• Paper 3, Section II, J

  Stochastic Financial Models

  Part II, 2017

  (a) State the fundamental theorem of asset pricing for a multi-period model.

  Consider a market model in which there is no arbitrage, the prices for all European put and call options are already known and there is a riskless asset $S^{0}=\left(S_{t}^{0}\right)_{t \in\{0, \ldots, T\}}$ with $S_{t}^{0}=(1+r)^{t}$ for some $r \geqslant 0$. The holder of a so-called 'chooser option' $C\left(K, t_{0}, T\right)$ has the right to choose at a preassigned time $t_{0} \in\{0,1, \ldots, T\}$ between a European call and a European put option on the same asset $S^{1}$, both with the same strike price $K$ and the same maturity $T$. [We assume that at time $t_{0}$ the holder will take the option having the higher price at that time.]

  (b) Show that the payoff function of the chooser option is given by

  $$C\left(K, t_{0}, T\right)= \begin{cases}\left(S_{T}^{1}-K\right)^{+} & \text {if } S_{t_{0}}^{1}>K(1+r)^{t_{0}-T} \\ \left(K-S_{T}^{1}\right)^{+} & \text {otherwise }\end{cases}$$

  (c) Show that the price $\pi\left(C\left(K, t_{0}, T\right)\right)$ of the chooser option $C\left(K, t_{0}, T\right)$ is given by

  $$\pi\left(C\left(K, t_{0}, T\right)\right)=\pi(E C(K, T))+\pi\left(E P\left(K(1+r)^{t_{0}-T}, t_{0}\right)\right),$$

  where $\pi(E C(K, T))$ and $\pi(E P(K, T))$ denote the price of a European call and put option, respectively, with strike $K$ and maturity $T$.

  comment

• Paper 4, Section II, J

  Stochastic Financial Models

  Part II, 2017

  (a) Describe the (Cox-Ross-Rubinstein) binomial model. When is the model arbitragefree? How is the equivalent martingale measure characterised in this case?

  (b) What is the price and the hedging strategy for any given contingent claim $C$ in the binomial model?

  (c) For any fixed $0<t<T$ and $K>0$, the payoff function of a forward-start-option is given by

  $$\left(\frac{S_{T}^{1}}{S_{t}^{1}}-K\right)^{+}$$

  Find a formula for the price of the forward-start-option in the binomial model.

  comment

• Paper 1, Section II, J

  Stochastic Financial Models

  Part II, 2017

  (a) What does it mean to say that $\left(X_{n}, \mathcal{F}_{n}\right)_{n \geqslant 0}$ is a martingale?

  (b) Let $\Delta_{0}, \Delta_{1}, \ldots$ be independent random variables on $(\Omega, \mathcal{F}, \mathbb{P})$ with $\mathbb{E}\left[\left|\Delta_{i}\right|\right]<\infty$ and $\mathbb{E}\left[\Delta_{i}\right]=0, i \geqslant 0$. Further, let

  $$X_{0}=\Delta_{0} \quad \text { and } \quad X_{n+1}=X_{n}+\Delta_{n+1} f_{n}\left(X_{0}, \ldots, X_{n}\right), \quad n \geqslant 0$$

  where

  $$f_{n}\left(x_{0}, \ldots, x_{n}\right)=\frac{1}{n+1} \sum_{i=0}^{n} x_{i}$$

  Show that $\left(X_{n}\right)_{n \geqslant 0}$ is a martingale with respect to the natural filtration $\mathcal{F}_{n}=$ $\sigma\left(X_{0}, \ldots, X_{n}\right)$.

  (c) State and prove the optional stopping theorem for a bounded stopping time $\tau$.

  comment

• Paper 4, Section II, K

  Stochastic Financial Models

  Part II, 2018

  Consider a utility function $U: \mathbb{R} \rightarrow \mathbb{R}$, which is assumed to be concave, strictly increasing and twice differentiable. Further, $U$ satisfies

  $$\left|U^{\prime}(x)\right| \leqslant c|x|^{\alpha}, \quad \forall x \in \mathbb{R},$$

  for some positive constants $c$ and $\alpha$. Let $X$ be an $\mathcal{N}\left(\mu, \sigma^{2}\right)$-distributed random variable and set $f(\mu, \sigma):=\mathbb{E}[U(X)]$.

  (a) Show that

  $$\mathbb{E}\left[U^{\prime}(X)(X-\mu)\right]=\sigma^{2} \mathbb{E}\left[U^{\prime \prime}(X)\right]$$

  (b) Show that $\frac{\partial f}{\partial \mu}>0$ and $\frac{\partial f}{\partial \sigma} \leqslant 0$. Discuss this result in the context of meanvariance analysis.

  (c) Show that $f$ is concave in $\mu$ and $\sigma$, i.e. check that the matrix of second derivatives is negative semi-definite. [You may use without proof the fact that if a $2 \times 2$ matrix has nonpositive diagonal entries and a non-negative determinant, then it is negative semi-definite.]

  comment

• Paper 3, Section II, $29 K$

  Stochastic Financial Models

  Part II, 2018

  Consider a multi-period model with asset prices $\bar{S}_{t}=\left(S_{t}^{0}, \ldots, S_{t}^{d}\right), t \in\{0, \ldots, T\}$, modelled on a probability space $(\Omega, \mathcal{F}, \mathbb{P})$ and adapted to a filtration $\left(\mathcal{F}_{t}\right)_{t \in\{0, \ldots, T\}}$. Assume that $\mathcal{F}_{0}$ is $\mathbb{P}$-trivial, i.e. $\mathbb{P}[A] \in\{0,1\}$ for all $A \in \mathcal{F}_{0}$, and assume that $S^{0}$ is a $\mathbb{P}$-a.s. strictly positive numéraire, i.e. $S_{t}^{0}>0 \mathbb{P}$-a.s. for all $t \in\{0, \ldots, T\}$. Further, let $X_{t}=\left(X_{t}^{1}, \ldots, X_{t}^{d}\right)$ denote the discounted price process defined by $X_{t}^{i}:=S_{t}^{i} / S_{t}^{0}, t \in\{0, \ldots, T\}, i \in\{1, \ldots, d\}$.

  (a) What does it mean to say that a self-financing strategy $\bar{\theta}$ is an arbitrage?

  (b) State the fundamental theorem of asset pricing.

  (c) Let $\mathbb{Q}$ be a probability measure on $(\Omega, \mathcal{F})$ which is equivalent to $\mathbb{P}$ and for which $\mathbb{E}_{\mathbb{Q}}\left[\left|X_{t}\right|\right]<\infty$ for all $t$. Show that the following are equivalent:

  (i) $\mathbb{Q}$ is a martingale measure.

  (ii) If $\bar{\theta}=\left(\theta^{0}, \theta\right)$ is self-financing and $\theta$ is bounded, i.e. $\max _{t=1, \ldots, T}\left|\theta_{t}\right| \leqslant c<\infty$ for a suitable $c>0$, then the value process $V$ of $\bar{\theta}$ is a $\mathbb{Q}$-martingale.

  (iii) If $\bar{\theta}=\left(\theta^{0}, \theta\right)$ is self-financing and $\theta$ is bounded, then the value process $V$ of $\bar{\theta}$ satisfies

  $$\mathbb{E}_{\mathbb{Q}}\left[V_{T}\right]=V_{0}$$

  [Hint: To show that (iii) implies (i) you might find it useful to consider self-financing strategies $\bar{\theta}=\left(\theta^{0}, \theta\right)$ with $\theta$ of the form

  $$\theta_{s}:= \begin{cases}\mathbf{1}_{A} & \text { if } s=t \\ 0 & \text { otherwise }\end{cases}$$

  for any $A \in \mathcal{F}_{t-1}$ and any $t \in\{1, \ldots, T\}$.]

  (d) Prove that if there exists a martingale measure $\mathbb{Q}$ satisfying the conditions in (c) then there is no arbitrage.

  comment

• Paper 2, Section II, K

  Stochastic Financial Models

  Part II, 2018

  Consider the Black-Scholes model, i.e. a market model with one risky asset with price $S_{t}$ at time $t$ given by

  $$S_{t}=S_{0} \exp \left(\sigma B_{t}+\mu t\right),$$

  where $\left(B_{t}\right)_{t \geqslant 0}$ denotes a Brownian motion on $(\Omega, \mathcal{F}, \mathbb{P}), \mu>0$ the constant growth rate, $\sigma>0$ the constant volatility and $S_{0}>0$ the initial price of the asset. Assume that the riskless rate of interest is $r \geqslant 0$.

  (a) Consider a European option $C=f\left(S_{T}\right)$ with expiry $T>0$ for any bounded, continuous function $f: \mathbb{R} \rightarrow \mathbb{R}$. Use the Cameron-Martin theorem to characterize the equivalent martingale measure and deduce the following formula for the price $\pi_{C}$ of $C$ at time 0 :

  $$\pi_{C}=e^{-r T} \int_{-\infty}^{\infty} f\left(S_{0} \exp \left(\sigma \sqrt{T} y+\left(r-\frac{1}{2} \sigma^{2}\right) T\right)\right) \frac{1}{\sqrt{2 \pi}} e^{-y^{2} / 2} d y$$

  (b) Find the price at time 0 of a European option with maturity $T>0$ and payoff $C=\left(S_{T}\right)^{\gamma}$ for some $\gamma>1$. What is the value of the option at any time $t \in[0, T] ?$ Determine a hedging strategy (you only need to specify how many units of the risky asset are held at any time $t$ ).

  comment

• Paper 1, Section II, K

  Stochastic Financial Models

  Part II, 2018

  (a) What does it mean to say that $\left(M_{n}, \mathcal{F}_{n}\right)_{n \geqslant 0}$ is a martingale?

  (b) Let $Y_{1}, Y_{2}, \ldots$ be independent random variables on $(\Omega, \mathcal{F}, \mathbb{P})$ with $Y_{i}>0 \mathbb{P}$-a.s. and $\mathbb{E}\left[Y_{i}\right]=1, i \geqslant 1$. Further, let

  $$M_{0}=1 \quad \text { and } \quad M_{n}=\prod_{i=1}^{n} Y_{i}, \quad n \geqslant 1$$

  Show that $\left(M_{n}\right)_{n \geqslant 0}$ is a martingale with respect to the filtration $\mathcal{F}_{n}=\sigma\left(Y_{1}, \ldots, Y_{n}\right)$.

  (c) Let $X=\left(X_{n}\right)_{n \geqslant 0}$ be an adapted process with respect to a filtration $\left(\mathcal{F}_{n}\right)_{n \geqslant 0}$ such that $\mathbb{E}\left[\left|X_{n}\right|\right]<\infty$ for every $n$. Show that $X$ admits a unique decomposition

  $$X_{n}=M_{n}+A_{n}, \quad n \geqslant 0,$$

  where $M=\left(M_{n}\right)_{n \geqslant 0}$ is a martingale and $A=\left(A_{n}\right)_{n \geqslant 0}$ is a previsible process with $A_{0}=0$, which can recursively be constructed from $X$ as follows,

  $$A_{0}:=0, \quad A_{n+1}-A_{n}:=\mathbb{E}\left[X_{n+1}-X_{n} \mid \mathcal{F}_{n}\right]$$

  (d) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a super-martingale. Show that the following are equivalent:

  (i) $\left(X_{n}\right)_{n \geqslant 0}$ is a martingale.

  (ii) $\mathbb{E}\left[X_{n}\right]=\mathbb{E}\left[X_{0}\right]$ for all $n \in \mathbb{N}$.

  comment

• Paper 4, Section II, K

  Stochastic Financial Models

  Part II, 2019

  (a) Describe the (Cox-Ross-Rubinstein) binomial model. What are the necessary and sufficient conditions on the model parameters for it to be arbitrage-free? How is the equivalent martingale measure $\mathbb{Q}$ characterised in this case?

  (b) Consider a discounted claim $H$ of the form $H=h\left(S_{0}^{1}, S_{1}^{1}, \ldots, S_{T}^{1}\right)$ for some function $h$. Show that the value process of $H$ is of the form

  $$V_{t}(\omega)=v_{t}\left(S_{0}^{1}, S_{1}^{1}(\omega), \ldots, S_{t}^{1}(\omega)\right)$$

  for $t \in\{0, \ldots, T\}$, where the function $v_{t}$ is given by

  $$v_{t}\left(x_{0}, \ldots, x_{t}\right)=\mathbb{E}_{\mathbb{Q}}\left[h\left(x_{0}, \ldots, x_{t}, x_{t} \cdot \frac{S_{1}^{1}}{S_{0}^{1}}, \ldots, x_{t} \cdot \frac{S_{T-t}^{1}}{S_{0}^{1}}\right)\right]$$

  You may use any property of conditional expectations without proof.

  (c) Suppose that $H=h\left(S_{T}^{1}\right)$ only depends on the terminal value $S_{T}^{1}$ of the stock price. Derive an explicit formula for the value of $H$ at time $t \in\{0, \ldots, T\}$.

  (d) Suppose that $H$ is of the form $H=h\left(S_{T}^{1}, M_{T}\right)$, where $M_{t}:=\max _{s \in\{0, \ldots, t\}} S_{s}^{1}$. Show that the value process of $H$ is of the form

  $$V_{t}(\omega)=v_{t}\left(S_{t}^{1}(\omega), M_{t}(\omega)\right)$$

  for $t \in\{0, \ldots, T\}$, where the function $v_{t}$ is given by

  $$v_{t}(x, m)=\mathbb{E}_{\mathbb{Q}}\left[g\left(x, m, S_{0}^{1}, S_{T-t}^{1}, M_{T-t}\right)\right]$$

  for a function $g$ to be determined.

  comment

• Paper 3, Section II, K

  Stochastic Financial Models

  Part II, 2019

  In the Black-Scholes model the price $\pi(C)$ at time 0 for a European option of the form $C=f\left(S_{T}\right)$ with maturity $T>0$ is given by

  $$\pi(C)=e^{-r T} \int_{-\infty}^{\infty} f\left(S_{0} \exp \left(\sigma \sqrt{T} y+\left(r-\frac{1}{2} \sigma^{2}\right) T\right)\right) \frac{1}{\sqrt{2 \pi}} e^{-y^{2} / 2} d y$$

  (a) Find the price at time 0 of a European call option with maturity $T>0$ and strike price $K>0$ in terms of the standard normal distribution function. Derive the put-call parity to find the price of the corresponding European put option.

  (b) The digital call option with maturity $T>0$ and strike price $K>0$ has payoff given by

  $$C_{\mathrm{digCall}}= \begin{cases}1 & \text { if } S_{T} \geqslant K \\ 0 & \text { otherwise }\end{cases}$$

  What is the value of the option at any time $t \in[0, T]$ ? Determine the number of units of the risky asset that are held in the hedging strategy at time $t$.

  (c) The digital put option with maturity $T>0$ and strike price $K>0$ has payoff

  $$C_{\text {digPut }}= \begin{cases}1 & \text { if } S_{T}<K \\ 0 & \text { otherwise. }\end{cases}$$

  Find the put-call parity for digital options and deduce the Black-Scholes price at time 0 for a digital put.

  comment

• Paper 2, Section II, $29 K$

  Stochastic Financial Models

  Part II, 2019

  (a) In the context of a multi-period model in discrete time, what does it mean to say that a probability measure is an equivalent martingale measure?

  (b) State the fundamental theorem of asset pricing.

  (c) Consider a single-period model with one risky asset $S^{1}$ having initial price $S_{0}^{1}=1$. At time 1 its value $S_{1}^{1}$ is a random variable on $(\Omega, \mathcal{F}, \mathbb{P})$ of the form

  $$S_{1}^{1}=\exp (\sigma Z+m), \quad m \in \mathbb{R}, \sigma>0,$$

  where $Z \sim \mathcal{N}(0,1)$. Assume that there is a riskless numéraire $S^{0}$ with $S_{0}^{0}=S_{1}^{0}=1$. Show that there is no arbitrage in this model.

  [Hint: You may find it useful to consider a density of the form $\exp (\tilde{\sigma} Z+\tilde{m})$ and find suitable $\tilde{m}$ and $\tilde{\sigma}$. You may use without proof that if $X$ is a normal random variable then $\mathbb{E}\left(e^{X}\right)=\exp \left(\mathbb{E}(X)+\frac{1}{2} \operatorname{Var}(X)\right)$.]

  (d) Now consider a multi-period model with one risky asset $S^{1}$ having a non-random initial price $S_{0}^{1}=1$ and a price process $\left(S_{t}^{1}\right)_{t \in\{0, \ldots, T\}}$ of the form

  $$S_{t}^{1}=\prod_{i=1}^{t} \exp \left(\sigma_{i} Z_{i}+m_{i}\right), \quad m_{i} \in \mathbb{R}, \sigma_{i}>0$$

  where $Z_{i}$ are i.i.d. $\mathcal{N}(0,1)$-distributed random variables on $(\Omega, \mathcal{F}, \mathbb{P})$. Assume that there is a constant riskless numéraire $S^{0}$ with $S_{t}^{0}=1$ for all $t \in\{0, \ldots, T\}$. Show that there exists no arbitrage in this model.

  comment

• Paper 1, Section II, 30K

  Stochastic Financial Models

  Part II, 2019

  (a) What does it mean to say that $\left(M_{n}, \mathcal{F}_{n}\right)_{n \geqslant 0}$ is a martingale? (b) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a Markov chain defined by $X_{0}=0$ and

  $$\begin{aligned} & \mathbb{P}\left[X_{n}=0 \mid X_{n-1}=0\right]=1-\frac{1}{n} \end{aligned}$$

  $$\begin{aligned} &\mathbb{P}\left[X_{n}=1 \mid X_{n-1}=0\right]=\mathbb{P}\left[X_{n}=-1 \mid X_{n-1}=0\right]=\frac{1}{2 n} \\ &\mathbb{P}\left[X_{n}=0 \mid X_{n-1}=0\right]=1-\frac{1}{n} \end{aligned}$$

  and

  $$\mathbb{P}\left[X_{n}=n X_{n-1} \mid X_{n-1} \neq 0\right]=\frac{1}{n}, \quad \mathbb{P}\left[X_{n}=0 \mid X_{n-1} \neq 0\right]=1-\frac{1}{n}$$

  for $n \geqslant 1$. Show that $\left(X_{n}\right)_{n \geqslant 0}$ is a martingale with respect to the filtration $\left(\mathcal{F}_{n}\right)_{n} \geqslant 0$ where $\mathcal{F}_{0}$ is trivial and $\mathcal{F}_{n}=\sigma\left(X_{1}, \ldots, X_{n}\right)$ for $n \geqslant 1$.

  (c) Let $M=\left(M_{n}\right)_{n \geqslant 0}$ be adapted with respect to a filtration $\left(\mathcal{F}_{n}\right)_{n \geqslant 0}$ with $\mathbb{E}\left[\left|M_{n}\right|\right]<\infty$ for all $n$. Show that the following are equivalent:

  (i) $M$ is a martingale.

  (ii) For every stopping time $\tau$, the stopped process $M^{\tau}$ defined by $M_{n}^{\tau}:=M_{n \wedge \tau}$, $n \geqslant 0$, is a martingale.

  (iii) $\mathbb{E}\left[M_{n \wedge \tau}\right]=\mathbb{E}\left[M_{0}\right]$ for all $n \geqslant 0$ and every stopping time $\tau$.

  [Hint: To show that (iii) implies (i) you might find it useful to consider the stopping time

  $$T(\omega):= \begin{cases}n & \text { if } \omega \in A, \\ n+1 & \text { if } \omega \notin A,\end{cases}$$

  for any $\left.A \in \mathcal{F}_{n .} .\right]$

  comment

• Paper 1, Section II, 30K

  Stochastic Financial Models

  Part II, 2020

  Consider a single-period asset price model $\left(\bar{S}_{0}, \bar{S}_{1}\right)$ in $\mathbb{R}^{d+1}$ where, for $n=0,1$,

  $$\bar{S}_{n}=\left(S_{n}^{0}, S_{n}\right)=\left(S_{n}^{0}, S_{n}^{1}, \ldots, S_{n}^{d}\right)$$

  with $S_{0}$ a non-random vector in $\mathbb{R}^{d}$ and

  $$S_{0}^{0}=1, \quad S_{1}^{0}=1+r, \quad S_{1} \sim N(\mu, V) .$$

  Assume that $V$ is invertible. An investor has initial wealth $w_{0}$ which is invested in the market at time 0 , to hold $\theta^{0}$ units of the riskless asset $S^{0}$ and $\theta^{i}$ units of risky asset $i$, for $i=1, \ldots, d$.

  (a) Show that in order to minimize the variance of the wealth $\bar{\theta} \cdot \bar{S}_{1}$ held at time 1 , subject to the constraint

  $$\mathbb{E}\left(\bar{\theta} \cdot \bar{S}_{1}\right)=w_{1}$$

  with $w_{1}$ given, the investor should choose a portfolio of the form

  $$\theta=\lambda \theta_{m}, \quad \theta_{m}=V^{-1}\left(\mu-(1+r) S_{0}\right)$$

  where $\lambda$ is to be determined.

  (b) Show that the same portfolio is optimal for a utility-maximizing investor with CARA utility function

  $$U(x)=-\exp \{-\gamma x\}$$

  for a unique choice of $\gamma$, also to be determined.

  comment

• Paper 2, Section II, 29K

  Stochastic Financial Models

  Part II, 2020

  Let $\left(S_{n}^{0}, S_{n}\right)_{0 \leqslant n \leqslant T}$ be a discrete-time asset price model in $\mathbb{R}^{d+1}$ with numéraire.

  (i) What is meant by an arbitrage for such a model?

  (ii) What does it mean to say that the model is complete?

  Consider now the case where $d=1$ and where

  $$S_{n}^{0}=(1+r)^{n}, \quad S_{n}=S_{0} \prod_{k=1}^{n} Z_{k}$$

  for some $r>0$ and some independent positive random variables $Z_{1}, \ldots, Z_{T}$ with $\log Z_{n} \sim N\left(\mu, \sigma^{2}\right)$ for all $n$.

  (iii) Find an equivalent probability measure $\mathbb{P}^{*}$ such that the discounted asset price $\left(S_{n} / S_{n}^{0}\right)_{0 \leqslant n \leqslant T}$ is a martingale.

  (iv) Does this model have an arbitrage? Justify your answer.

  (v) By considering the contingent claim $\left(S_{1}\right)^{2}$ or otherwise, show that this model is not complete.

  comment

• Paper 3, Section II, 29K

  Stochastic Financial Models

  Part II, 2020

  (a) Let $\left(B_{t}\right)_{t \geqslant 0}$ be a real-valued random process.

  (i) What does it mean to say that $\left(B_{t}\right)_{t \geqslant 0}$ is a Brownian motion?

  (ii) State the reflection principle for Brownian motion.

  (b) Suppose that $\left(B_{t}\right)_{t \geqslant 0}$ is a Brownian motion and set $M_{t}=\sup _{s \leqslant t} B_{s}$ and $Z_{t}=M_{t}-B_{t}$.

  (i) Find the joint distribution function of $B_{t}$ and $M_{t}$.

  (ii) Show that $\left(M_{t}, Z_{t}\right)$ has a joint density function on $[0, \infty)^{2}$ given by

  $$\mathbb{P}\left(M_{t} \in d y \text { and } Z_{t} \in d z\right)=\frac{2}{\sqrt{2 \pi t}} \frac{(y+z)}{t} e^{-(y+z)^{2} /(2 t)} d y d z$$

  (iii) You are given that two of the three processes $\left(\left|B_{t}\right|\right)_{t \geqslant 0},\left(M_{t}\right)_{t \geqslant 0}$ and $\left(Z_{t}\right)_{t \geqslant 0}$ have the same distribution. Identify which two, justifying your answer.

  comment

• Paper 4, Section II, K

  Stochastic Financial Models

  Part II, 2020

  (i) What does it mean to say that $\left(S_{t}^{0}, S_{t}\right)_{0 \leqslant t \leqslant T}$ is a Black-Scholes model with interest rate $r$, drift $\mu$ and volatility $\sigma$ ?

  (ii) Write down the Black-Scholes pricing formula for the time- 0 value $V_{0}$ of a time- $T$ contingent claim $C$.

  (iii) Show that if $C$ is a European call of strike $K$ and maturity $T$ then

  $$V_{0} \geqslant S_{0}-e^{-r T} K$$

  (iv) For the European call, derive the Black-Scholes pricing formula

  $$V_{0}=S_{0} \Phi\left(d^{+}\right)-e^{-r T} K \Phi\left(d^{-}\right)$$

  where $\Phi$ is the standard normal distribution function and $d^{+}$and $d^{-}$are to be determined.

  (v) Fix $t \in(0, T)$ and consider a modified contract which gives the investor the right but not the obligation to buy one unit of the risky asset at price $K$, either at time $t$ or time $T$ but not both, where the choice of exercise time is to be made by the investor at time $t$. Determine whether the investor should exercise the contract at time $t$.

  comment

• Paper 1, Section II, 30K

  Stochastic Financial Models

  Part II, 2021

  (a) What does it mean to say that a stochastic process $\left(X_{n}\right)_{n \geqslant 0}$ is a martingale with respect to a filtration $\left(\mathcal{F}_{n}\right)_{n \geqslant 0}$ ?

  (b) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a martingale, and let $\xi_{n}=X_{n}-X_{n-1}$ for $n \geqslant 1$. Suppose $\xi_{n}$ takes values in the set $\{-1,+1\}$ almost surely for all $n \geqslant 1$. Show that $\left(X_{n}\right)_{n \geqslant 0}$ is a simple symmetric random walk, i.e. that the sequence $\left(\xi_{n}\right)_{n \geqslant 1}$ is $\operatorname{IID}$ with $\mathbb{P}\left(\xi_{1}=1\right)=1 / 2=$ $\mathbb{P}\left(\xi_{1}=-1\right) .$

  (c) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a martingale and let the bounded process $\left(H_{n}\right)_{n \geqslant 1}$ be previsible.

  Let $\hat{X}_{0}=0$ and

  $$\hat{X}_{n}=\sum_{k=1}^{n} H_{k}\left(X_{k}-X_{k-1}\right) \text { for } n \geqslant 1$$

  Show that $\left(\hat{X}_{n}\right)_{n \geqslant 0}$ is a martingale.

  (d) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a simple symmetric random walk with $X_{0}=0$, and let

  $$T_{a}=\inf \left\{n \geqslant 0: X_{n}=a\right\}$$

  where $a$ is a positive integer. Let

  $$\hat{X}_{n}= \begin{cases}X_{n} & \text { if } n \leqslant T_{a} \\ 2 a-X_{n} & \text { if } n>T_{a}\end{cases}$$

  Show that $\left(\hat{X}_{n}\right)_{n \geqslant 0}$ is a simple symmetric random walk.

  (e) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a simple symmetric random walk with $X_{0}=0$, and let $M_{n}=\max _{0 \leqslant k \leqslant n} X_{k}$. Compute $\mathbb{P}\left(M_{n}=a\right)$ for a positive integer $a$.

  comment

• Paper 2, Section II, 30K

  Stochastic Financial Models

  Part II, 2021

  Consider a one-period market model with $d$ risky assets and one risk-free asset. Let $S_{t}$ denote the vector of prices of the risky assets at time $t \in\{0,1\}$ and let $r$ be the interest rate.

  (a) What does it mean to say a portfolio $\varphi \in \mathbb{R}^{d}$ is an arbitrage for this market?

  (b) An investor wishes to maximise their expected utility of time-1 wealth $X_{1}$ attainable by investing in the market with their time- 0 wealth $X_{0}=x$. The investor's utility function $U$ is increasing and concave. Show that, if there exists an optimal solution $X_{1}^{*}$ to the investor's expected utility maximisation problem, then the market has no arbitrage. [Assume that $U\left(X_{1}\right)$ is integrable for any attainable time-1 wealth $X_{1}$.]

  (c) Now introduce a contingent claim with time-1 bounded payout $Y$. How does the investor in part (b) calculate an indifference bid price $\pi(Y)$ for the claim? Assuming each such claim has a unique indifference price, show that the map $Y \mapsto \pi(Y)$ is concave. [Assume that any relevant utility maximisation problem that you consider has an optimal solution.]

  (d) Consider a contingent claim with time-1 bounded payout $Y$. Let $I \subseteq \mathbb{R}$ be the set of initial no-arbitrage prices for the claim; that is, the set $I$ consists of all $p$ such that the market augmented with the contingent claim with time- 0 price $p$ has no arbitrage. Show that $\pi(Y) \leqslant \sup \{p \in I\}$. [Assume that any relevant utility maximisation problem that you consider has an optimal solution. You may use results from lectures without proof, such as the fundamental theorem of asset pricing or the existence of marginal utility prices, as long as they are clearly stated.]

  comment

• Paper 3, Section II, 29K

  Stochastic Financial Models

  Part II, 2021

  (a) Let $M=\left(M_{n}\right)_{n \geqslant 0}$ be a martingale and $\hat{M}=\left(\hat{M}_{n}\right)_{n \geqslant 0}$ a supermartingale. If $M_{0}=\hat{M}_{0}$, show that $\mathbb{E}\left(M_{T}\right) \geqslant \mathbb{E}\left(\hat{M}_{T}\right)$ for any bounded stopping time $T$. [If you use a general result about supermartingales, you must prove it.]

  (b) Consider a market with one stock with time- $n$ price $S_{n}$ and constant interest rate $r$. Explain why a self-financing investor's wealth process $\left(X_{n}\right)_{n \geqslant 0}$ satisfies

  $$X_{n}=(1+r) X_{n-1}+\theta_{n}\left[S_{n}-(1+r) S_{n-1}\right]$$

  where $\theta_{n}$ is the number of shares of the stock held during the $n$th period.

  (c) Given an initial wealth $X_{0}$, an investor seeks to maximize $\mathbb{E}\left[U\left(X_{N}\right)\right]$, where $U$ is a given utility function. Suppose the stock price is such that $S_{n}=S_{n-1} \xi_{n}$, where $\left(\xi_{n}\right)_{n \geqslant 1}$ is a sequence of independent copies of a random variable $\xi$. Let $V$ be defined inductively by

  $$V(n-1, x)=\sup _{t \in \mathbb{R}} \mathbb{E}[V(n,(1+r) x+t(1+r-\xi))]$$

  with terminal condition $V(N, x)=U(x)$ for all $x \in \mathbb{R}$.

  Show that the process $\left(V\left(n, X_{n}\right)\right)_{0 \leqslant n \leqslant N}$ is a supermartingale for any trading strategy $\left(\theta_{n}\right)_{1 \leqslant n \leqslant N}$. Suppose that the trading strategy $\left(\theta_{n}^{*}\right)_{1 \leqslant n \leqslant N}$ with corresponding wealth process $\left(X_{n}^{*}\right)_{0 \leqslant n \leqslant N}$ are such that the process $\left(V\left(n, X_{n}^{*}\right)\right)_{0 \leqslant n \leqslant N}$ is a martingale. Show that $\left(\theta_{n}^{*}\right)_{1 \leqslant n \leqslant N}$ is optimal.

  comment

• Paper 4, Section II, 29K

  Stochastic Financial Models

  Part II, 2021

  (a) What does it mean to say that a stochastic process is a Brownian motion? Show that, if $\left(W_{t}\right)_{t \geqslant 0}$ is a continuous Gaussian process such that $\mathbb{E}\left(W_{t}\right)=0$ and $\mathbb{E}\left(W_{s} W_{t}\right)=s$ for all $0 \leqslant s \leqslant t$, then $\left(W_{t}\right)_{t \geqslant 0}$ is a Brownian motion.

  For the rest of the question, let $\left(W_{t}\right)_{t \geqslant 0}$ be a Brownian motion.

  (b) Let $\widehat{W}_{0}=0$ and $\widehat{W}_{t}=t W_{1 / t}$ for $t>0$. Show that $\left(\widehat{W}_{t}\right)_{t \geqslant 0}$ is a Brownian motion. [You may use without proof the Brownian strong law of large numbers: $W_{t} / t \rightarrow 0$ almost surely as $t \rightarrow \infty$.]

  (c) Fix constants $c \in \mathbb{R}$ and $T>0$. Show that

  $$\mathbb{E}\left[f\left(\left(W_{t}+c t\right)_{0 \leqslant t \leqslant T}\right)\right]=\mathbb{E}\left[\exp \left(c W_{T}-\frac{1}{2} c^{2} T\right) f\left(\left(W_{t}\right)_{0 \leqslant t \leqslant T}\right)\right]$$

  for any bounded function $f: C[0, T] \rightarrow \mathbb{R}$ of the form

  $$f(\omega)=g\left(\omega\left(t_{1}\right), \ldots, \omega\left(t_{n}\right)\right),$$

  for some fixed $g$ and fixed $0<t_{1}<\ldots<t_{n}=T$, where $C[0, T]$ is the space of continuous functions on $[0, T]$. [If you use a general theorem from the lectures, you should prove it.]

  (d) Fix constants $x \in \mathbb{R}$ and $T>0$. Show that

  $$\mathbb{E}\left[f\left(\left(W_{t}+x\right)_{t \geqslant T}\right)\right]=\mathbb{E}\left[\exp \left((x / T) W_{T}-\frac{1}{2}\left(x^{2} / T\right)\right) f\left(\left(W_{t}\right)_{t \geqslant T}\right)\right]$$

  for any bounded function $f: C[T, \infty) \rightarrow \mathbb{R}$. [In this part you may use the Cameron-Martin theorem without proof.]

  comment